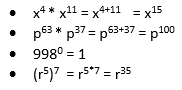Machtsverbanden

Machtsverbanden hebben alles te maken met enorm snelle groei- en krimpprocessen. Denk bijvoorbeeld aan de Bitcoin prijs: in 7 jaar ging de waarde van één bitcoin van minder dan een dollarcent naar 20.000 dollar. Of wat dacht je van de groei van de wereldbevolking? In 1700 waren er 600 miljoen mensen op de aarde, terwijl er nu bijna 8 miljard rondlopen. Om meer te weten over dit soort extreme groeiscenario's, moet je begrijpen hoe machtsverbanden werken. Daar leggen we je in dit artikel alles over uit.  

Wat is een machtsverband?

Een machtsverband is een verband waarbij een getal (a × x) steeds wordt vermenigvuldigd met een n aantal keren. In principe wordt dit vertegenwoordigd door de volgende formule:

y = a × xⁿ

waarbij:

• x = het grondtal
• n = de exponent

Dit is ook de formule van een evenredig verband met een macht.

Het steeds vermenigvuldigen van een getal met een n aantal keren wordt ook wel machtsverheffen genoemd. Machten zijn erg effectief in de wiskunde, omdat ze ervoor zorgen dat formules korter en overzichtelijker kunnen worden opgeschreven. Het meest bekende machtsverband is de macht 2, ook wel kwadraat genoemd: 2² = 2 × 2 = 4. Je kan ook verder gaan door dit nogmaals met 2 te vermenigvuldigen, dan krijg je dus twee tot de macht drie, in getallen: 2³ = 2 × 2 × 2 = 8. Hierbij is 2 het grondtal, en het getal rechtsboven de exponent. Het grondtal geeft aan van welk getal je de macht neemt, en de exponent geeft aan hoevaak het grondtal met zichzelf wordt vermenigvuldigd.

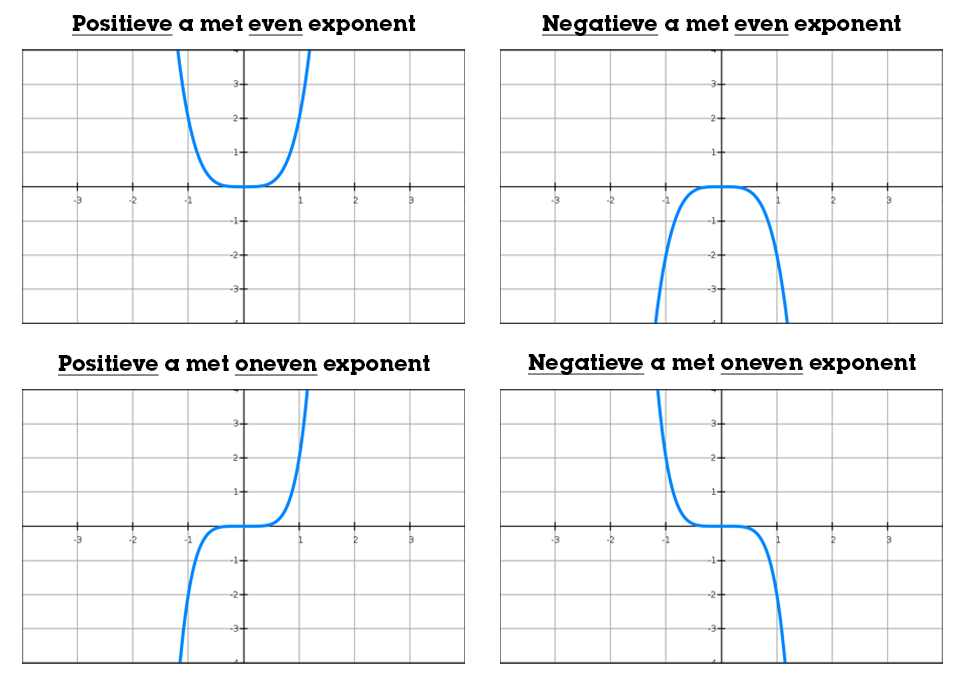
Bij machtsverbanden is het belangrijk om te weten dat de constante a zowel een positieve als negatieve vorm kan aannemen, terwijl de exponent n zowel een even als oneven getal kan zijn. Je krijgt dan vier verschillende combinaties met elk een bijbehorende grafiek die er anders uitziet:

Video

Wil je meer weten over hoe grafieken bij bepaalde machtsfuncties tot stand komen? Check dan onderstaande video van WiskundeAcademie.

Hoe stel je formules op bij machtsverbanden?

Het opstellen van formules bij machtsverbanden is goed om onder de knie te hebben. In deze sectie zullen we laten zien hoe dat gaat. Gegeven is bijvoorbeeld de formule y = a × x³. Zoals je ziet is de coëfficiënt a onbekend. Maar stel dat je wel weet dat voor x = 4, y = 320 geldt. Hoe stel je dan de formule op van y?

y = a × x³

x = 4 en y = 320

Dus 320 = a × 4³

We kunnen nu links en rechts delen door de macht 4³.

320 / 4³  = a

5 = a

Dus de formule van y luidt: y = 5 × x³

Het kan natuurlijk ook zijn dat de coëfficiënt wel gegeven is, maar de exponent niet. Neem bijvoorbeeld P = 120S^c en stel dat de volgende gegevens zijn gegeven: S = 4,8 en P = 840. De vraag is nu wat de waarde van exponent c is.

P = 120S^c                    

S = 4,8 en P = 840

Dus 840 = 120 × 4,8^c

Dit ziet er uit als een moeilijke formule waarbij je de c niet eenvoudigweg kan bepalen. Echter, er zijn 2 methodes om dit op te lossen. Welke methode je kiest hangt af van of de vergelijking algebraïsch / exact gevonden moet worden. Zo niet? Dan mag je hem oplossen door middel van je grafische rekenmachine te gebruiken. Dan vul je bij Y1 het linkerlid in, en bij Y2 het rechterlid. Vervolgens vind je het punt waar ze elkaar snijden (door intersect), en voila, je hebt de waarde van c!

De algebraïsche methode is iets uitgebreider, namelijk:

840 = 120 × 4,8^c

Zowel linker- als rechterlid delen door 120.

840 / 120 = 4,8^c

7 = 4,8^c

C = log(7)/log(4,8)

C ≈ 1,241

Dus de formule van P luidt: P = 120S^1,241

Video

In deze uitlegvideo's van WiskundeAcademie zie je nog een voorbeeld van hoe je een formule opstelt bij een machtsverband:

Hoe reken je met machtsverbanden?

Rekenen met machtsverbanden gaat, natuurlijk naast de algemene voorrangsregels in de wiskunde, volgens een aantal rekenregels. Die zijn als volgt:

In de praktijk kan dit er als volgt uitzien:

Uit deze voorbeelden kan worden afgeleid, dat ongeacht het grondgetal x, het antwoord altijd 1 is als de macht 0 is. Ook geldt dat a = b als g^a = g^b, zolang geldt dat g > 0 en g niet gelijk is aan 1. Let hierbij goed op, zoals je bij de eerste rekenregel kunt zien, dat alleen variabelen met het grondtal zijn op te tellen. z^a × g^b = g^a+b kan dus NIET!

Voorbeeld

Als voorbeeld nemen we de vergelijking y = 5 × x³. Stel, je wil weten wat de waarde van y is als x = 3. Hetgeen wat je dan doet is als volgt:

y = 5 × (3)³ = 135

y = 5 × 27 = 135

Om onduidelijkheden te voorkomen, is het handig om haakjes om het getal te plaatsen. Verder kun je natuurlijk een tabel opstellen als je de vergelijking van een machtsverband hebt. Bij bovenstaande formule hoort de volgende tabel:

x	y
0	0
1	5
2	40
3	135
4	320

 

Met behulp van een tabel kan je vervolgens eenvoudig een bijbehorende grafiek tekenen.

Wat is een exponentiële macht?

Bij een exponentiële macht wordt de hoeveelheid N steeds met hetzelfde getal vermenigvuldigd. Er is in dat geval sprake van een exponentiële toename. De algemene formule die bij een exponentiële functie hoort, luidt als volgt:

N = b × g^t

waarbij:

• b = beginwaarde
• g = groeifactor

Zoals je kunt zien zit er een machtsfunctie in de exponentiële functie. Bij een exponentiële functie neemt een bepaalde hoeveelheid met een vaste factor per tijdseenheid toe of af. Dit houdt in dat de waarde van N steeds sneller stijgt ofwel steeds sneller daalt.

Hoe reken je met een exponentiële macht?

Ook bij exponentiële machten werk je met de bovenstaande rekenregels. Stel, je wilt de verspreiding van een bepaald soort virus weten. Laten we aannemen dat bij kamertemperatuur het virus groeit volgens de gegevens uit onderstaande tabel.

Tijd (uren)	Hoeveelheid virus (mg)
0	6
1	12
2	24
3	48
4	96
5	192

 

Om uit de tabel de formule af te leiden, delen we de opeenvolgende waarden:

• 12/6 = 2
• 24/12 = 2
• 48/24 = 2
• 96/48 = 2
• 192/96 = 2

De hoeveelheid virus verspreidt zich dus exponentieel met een groeifactor van 2. Hier spreek je dus van exponentiële groei. Dit kun je ook afleiden doordat de ‘t’ de exponent is. Verder zien we hier dat de beginwaarde b = 6. De functie luidt dan als volgt:

Hoeveelheid virus = 6 × 2^Tijd

Wat is de e-macht?

De e-macht is een macht waarvan het grondgetal het getal e is. Het getal e is een wiskundige constante en het grondtal van de natuurlijke logaritme. De waarde van e is 2,71828. Het getal heet euler, verwijzend naar de ontdekker en wiskundige Leonhard Euler.