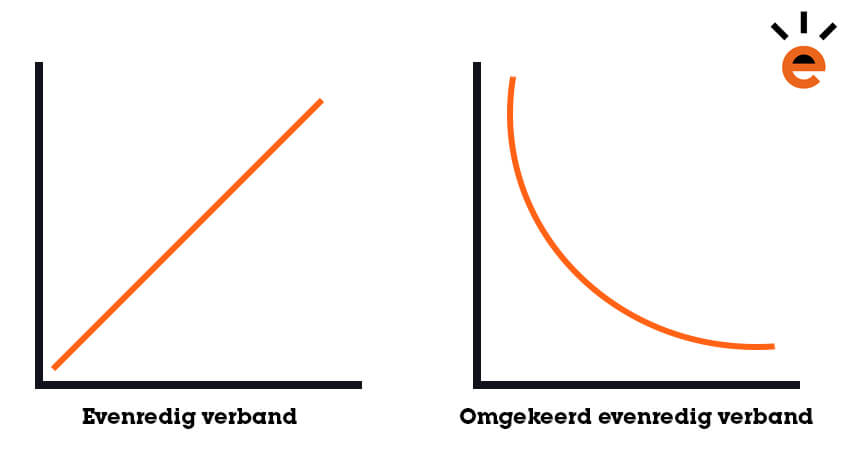
Evenredige verbanden

In de wiskunde kom je regelmatig evenredige verbanden tegen. Zo heb je recht evenredige verbanden, evenredige verbanden met een macht en omgekeerd evenredige verbanden. Wil je weten wat elk van deze verbanden precies inhoudt? In dit artikel lees je alles over evenredige verbanden!

Wat is een evenredig verband?

Bij een evenredig verband geldt 'hoe hoger a, hoe hoger b' en 'hoe lager a, hoe lager b'.

In het dagelijks leven komen we regelmatig situaties tegen waarin de waarde van een bepaalde grootheid wordt beïnvloed door de waarde van een andere grootheid. Zo wordt het brandstofverbruik van een auto onder andere beïnvloed door het gewicht van de auto. Hoe hoger het gewicht van de auto, hoe hoger het brandstofverbruik. Hier is de invloed op beide variabelen positief. We zeggen dan ook wel dat de richting van beide variabelen hetzelfde is. Dit heet een evenredig verband.

Aangezien a toeneemt als b dat doet en vice versa, blijft de directe verhouding van de overeenkomstige waarden constant. Dus als de waarden van b; b₁, b₂ overeenkomt met de waarden van a; a₁, a_2, dan is hun verhouding constant. Er geldt dan:

a₁ / b₁ = a₂ / b₂

De formule voor evenredige verbanden is:

a / b = k, waarbij k de evenredigheidsconstante is.

Recht evenredig verband

Een recht evenredig verband wordt aangegeven met y = ax. Dit is een lineaire vergelijking die begint in de oorsprong (0,0). Als de variabele x twee keer zo groot wordt, wordt de variabele y ook twee keer zo groot. Als de variabele x vier keer zo groot wordt, wordt de variabele y ook vier keer zo groot.

Evenredig verband met een macht

Een evenredig verband met een macht wordt aangegeven met y = axⁿ. Als n = 2, en de variabele x wordt twee keer zo groot, dan wordt y vier keer zo groot. 2² is immers 4. Als de variabele x vier keer zo groot wordt, dan wordt y 16 keer zo groot. Hier geldt namelijk ook 4² = 16.

Wat is een omgekeerd evenredig verband?

Bij een omgekeerd evenredig verband geldt 'hoe hoger a, hoe lager b' en 'hoe lager a, hoe hoger b'.

Hierbij bewegen variabelen dus in tegenovergestelde richting. 

De twee variabelen a en b zijn omgekeerd evenredig als:

• a ~ 1 / b        (~ betekent ‘is evenredig met / is proportioneel met’)
• ab = k; waarbij k de evenredigheidsconstante is

De evenredigheidsconstante is hier het getal dat telkens hetzelfde blijft als:

• a in waarde toeneemt en b in dezelfde waarde afneemt;
• a in waarde afneemt en b in dezelfde waarde toeneemt.

In dit geval veroorzaakt een toename van variabele b een afname van de waarde van variabele a. Net als dat een afname van variabele b een toename van de waarde van variabele a veroorzaakt. De noemer en het antwoord zijn omgekeerd evenredig.

Voorbeelden van een omgekeerd evenredig verband:

• Een sirene van een naderende brandweerauto die luider wordt naarmate het voertuig je nadert, maar stiller wordt als het verder weg van je gaat. Je merkt dus dat hoe kleiner de afstand tussen jou en het voertuig, hoe luider de sirene. Ook geldt dat hoe groter de afstand, hoe stiller de sirene wordt.
• De tijd die een bepaald aantal werknemers nodig heeft om een stuk werk te verrichten, varieert omgekeerd evenredig met het aantal werknemers. Dit betekent dat hoe kleiner het aantal werknemers, hoe meer tijd er nodig is om het werk af te maken en vice versa. Dus tijd ~ 1 / werknemers.
• De snelheid van een bewegend vaartuig zoals een trein, voertuig of schip varieert omgekeerd evenredig met de tijd die nodig is om een bepaalde afstand af te leggen. Hoe hoger de snelheid, hoe minder tijd het kost om de afstand af te leggen. Dus tijd ~ 1 / snelheid bewegend voertuig.

Video

Wil je de uitleg over evenredige verbanden nog eens rustig terugkijken? Bekijk dan zeker even onderstaande uitlegvideo van Math with Menno:

Oefenopgaven (omgekeerd) evenredige verbanden

Opgave 1

Sara koopt appelgebak. Als zij dit gebakje onder 6 mensen verdeelt, krijgt elk persoon 500 gram taart. Als ze 6000 gram appelgebak koopt, hoeveel krijgt ieder persoon dan?

Antwoord

• Bij 6 personen, ieder persoon 500 gram, bij totaal: 6*500 = 3000 gram
• Nu is er 6000 gram appeltaart. Dus 2 maal zo veel.
• Het aantal gram dat ieder persoon krijgt, is nu ook 2 maal zoveel. Dus: 2 * 500 gram = 1000 gram.

Opgave 2

35 boeren hebben 8 dagen nodig om koffie te oogsten op een plantage. Hoelang duurt het voordat 20 boeren koffie oogsten op dezelfde plantage?

Antwoord

• Duur van één werknemer = (35 × 8) dagen
• Bereken nu de duur van 20 arbeiders: (35 × 8) / 20 = 14 dagen
• Daarom zullen 20 arbeiders 14 dagen nodig hebben

Opgave 3

Het duurt 28 dagen voordat 6 geiten of 8 schapen een weiland grazen. Hoelang duurt het voordat 9 geiten en 2 schapen op hetzelfde veld grazen?

Antwoord

• 6 geiten = 8 schapen
• ⇒ 1 geit = 8/6 schapen
• ⇒ 9 geiten ≡ (8/6 × 9) schapen = 12 schapen
• ⇒ (9 geiten + 2 schapen) ≡ (12 schapen + 2 schapen) = 14 schapen
• Nu 8 schapen => 28 dagen
• Eén schaap zal binnen (28 × 8) dagen grazen
• ⇒ 14 schapen duren (28 × 8) / 14 dagen
• = 16 dagen
• Daarom hebben 9 geiten en 2 schapen 16 dagen nodig om op het veld te grazen.

Opgave 4

Negen kranen kunnen een tank in vier uur vullen. Hoelang duurt het twaalf vergelijkbare kranen om dezelfde tank te vullen?

Antwoord

• De verhoudingen zijn als volgt:
• x₁ / x₂ = y₂ / y₁
• ⇒ 9 / x = 12/4
• x = 3

Opgave 5

In de natuurkunde kunnen we de versnelling definiëren met de volgende formule: a = ∆v / t. Hieruit blijkt dat a en t omgekeerd evenredig zijn, aldus a ~ 1/t (bij veronderstelling constante ∆v). Stel nu dat de snelheidsverandering 30 m/s is. De tijd die een persoon hier over zou doen is 3 seconden. Dit zou betekenen dat de versnelling 10 m/s² is. Als de tijd die een persoon over 30 m/s zou doen, nu 6 seconden was in plaats van 3, wat zou dan de versnelling zijn?

Antwoord

• De tijd wordt 2 keer zo snel
• Dit betekent dat de versnelling twee keer zo klein wordt.
• 10/2 = 5 m/s²