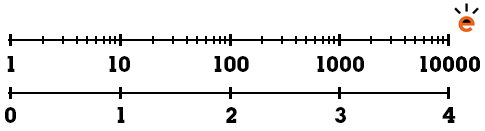Logaritmen

Grondgetallen, exponenten, 'verheffen tot': het zijn allemaal termen die te maken hebben met logaritmen en logaritmische functies. In dit artikel kun je lezen wat logaritmen precies zijn en hoe je ze gebruikt.

Wat is een logaritme?

Een logaritme is het tegenovergestelde van een exponent. Hierbij stel je jezelf de volgende vraag:

'Tot welke macht moet ik mijn grondgetal verheffen om dit getal in mijn logaritme te krijgen?'

De logaritme bestaat uit een paar onderdelen. In het onderstaande voorbeeld is 2 het grondgetal. Tussen de haakjes staat het getal wat zou ontstaan na het verheffen van het grondgetal tot een bepaalde macht. Tot welke macht moet ik 2 verheffen om 8 te krijgen? Het antwoord daarop is 3.

• log₂(8) = 3, want 2³ = 8

Het grondgetal wordt soms rechtsonder en soms linksboven het woord ‘log’ geschreven. Dat maakt inhoudelijk geen verschil.

Voor het grondgetal kun je in theorie alles invullen, maar er zijn een paar grondgetallen die vaak voorkomen: 10, 2 en e. De logaritme met als grondgetal e is bijzonder. Dat noemen we het natuurlijk logaritme en we schijven dan ln(x) in plaats van log_e(x).

Video

In onderstaande video legt WiskundeAcademie ook uit wat een logaritme precies is:

Rekenen met logaritmen

Om te begrijpen hoe de getallen in de logaritme met elkaar in verband staan, kun je een simpel logaritme opschrijven. Dit helpt als ezelbruggetje voor moeilijkere logaritmen:

• 2³ = 8
• log₂(8) = 3

Voor het rekenen met logaritmen moet je rekenregels kennen. Die regels worden hieronder uitgelegd.

Optellen/aftrekken

Om logaritmen op te tellen of van elkaar af te trekken is het in eerste instantie belangrijk dat deze logaritmen hetzelfde grondgetal hebben. Vervolgens vermenigvuldig je de getallen binnen de haakjes met elkaar in het geval van optellen. In het geval van aftrekken, deel je ze door elkaar.

• log(a) + log(b) = log(a × b)
• log(a) - log(b) = log(a / b)

Vermenigvuldigen met een constante

Als je een logaritme vermenigvuldigt met een ander getal, dan mag je dat andere getal binnen de haakjes halen en in de macht zetten. Dit kan helpen met het versimpelen van een wiskundig probleem. Het werkt natuurlijk allebei de kanten op. Dus je kunt ook het getal binnen de haakjes in een machtsvorm schijven en dan de macht buiten de logaritme halen.

• c × log(a) = log(a^c)

Voor een negatief getal ziet dat eruit zoals hieronder. Je verheft het getal binnen de haakjes tot een negatieve macht. Een negatieve macht is hetzelfde als diezelfde macht (maar dan positief) onder de deelstreep.

• -c × log(a) = log(a^-c) = log (1 / a^c)

Logaritmen delen (grondgetal wegwerken)

Niet op alle rekenmachines kun je zelf het grondgetal aanpassen. Als dat op jouw rekenmachine niet kan, gebruikt je rekenmachine waarschijnlijk automatisch 10 als grondgetal. Stel dat je een ander grondgetal g wil gebruiken, dan kun je de volgende rekenregel gebruiken:

Je deelt de logaritme van a door de logaritme van je gewenste grondgetal g.

Dat geeft hetzelfde resultaat als de logaritme van a met grondgetal g. Het maakt hier niet uit wat het grondgetal is van de twee logaritmen die je door elkaar deelt, zolang ze maar hetzelfde zijn.

• log_g(a) = log(a) / log(g)

Handig weetje: als je op je rekenmachine 'log' intikt zonder grondgetal te definiëren, dan zal hij 10 gebruiken als grondgetal. 

Logaritme in de macht

Als een logaritme in de macht staat, krijg je een interessante situatie. Kijk maar naar het onderstaande voorbeeld.

• b^logb(a) = a

Speciale gevallen

De logaritme van 1 is altijd 0. Dit is onafhankelijk van het grondgetal, omdat alles tot de macht 0 gelijk is aan 1.

• log(1) = 0

Als het grondgetal van de logaritme hetzelfde is als het grondgetal van een exponent binnen de logaritme, dan is het ook gemakkelijk op te lossen. Het antwoord op ‘tot welke macht moeten we a verheffen om a^b te krijgen?’ wijst zichzelf. Voor een macht van 1 is het nog duidelijker.

• log_a(a^b) = b
• log_a(a) = 1

Video

Check onderstaande uitlegvideo als je alle rekenregels (inclusief voorbeelden) nog een keer voorbij wil zien komen:

Waarom zijn logaritmen handig?

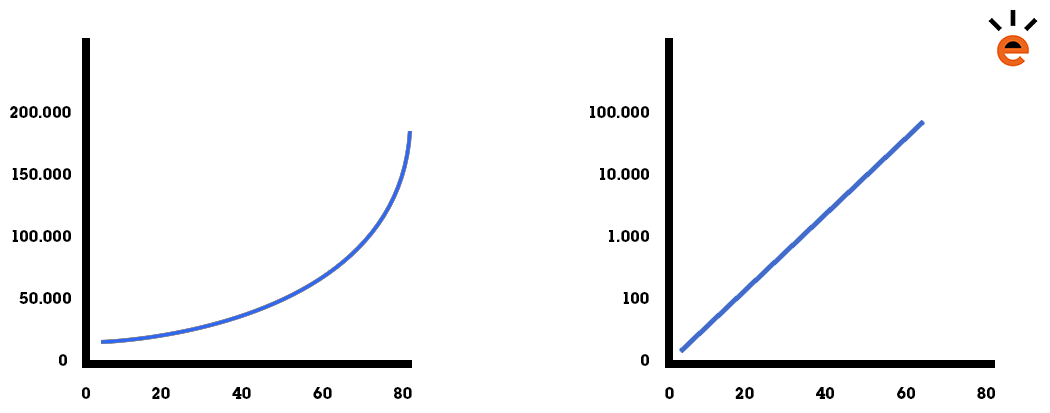
Logaritmen zijn handig om bepaalde verbanden makkelijker te visualiseren. Een logaritmische grafiek wordt bijvoorbeeld vaak gebruikt bij een prijs-analyse van Bitcoin. De prijs van deze munt is in de eerste jaren zo hard gestegen dat een logaritmische grafiek je veel meer informatie geeft dan een lineaire grafiek.

In de onderstaande grafieken is twee keer hetzelfde verband weergegeven. Het gaat in dit voorbeeld om een exponentiële groei. In de linker grafiek is een lineaire schaal gebruikt op beide assen, in de rechter grafiek is een logaritmische schaal gebruikt op de y-as. Het valt op dat de rechter grafiek makkelijker af te lezen is. Het is ook nog mogelijk om de x-as logaritmisch te maken, maar dat is in dit geval niet handig.

Wat is een logaritmische schaal?

Bij een logaritmische schaal wordt de exponent steeds één stapje groter, terwijl bij een lineaire schaal het getal steeds één stapje groter wordt. Het is gebruikelijk om hierbij het grondgetal 10 te gebruiken. Dat is ook wat wordt gebruikt op logaritmisch papier. De stapjes gaan dus als volgt: 10⁰, 10¹, 10², etc... Hieronder een voorbeeld van een logaritmische (bovenste) en een lineaire (onderste) as. De machten van 10 zijn uitgeschreven.

Tussen 10⁰ en 10¹ worden stapjes van 1 gezet, maar tussen 10¹ en 10² worden stapjes van 10 gezet, enzovoorts. De stapjes zijn dus steeds anders. Ook valt op dat ze geen gelijke sprongetjes maken op de as.