Lineaire verbanden

Elk uur dat jij in de supermarkt de schappen bijvult, verdien jij steeds hetzelfde bedrag. Na elke 365 dagen die verstrijken, gaat jouw leeftijd steeds met één omhoog. Dat zijn lineaire verbanden in de praktijk, maar wat houden ze wiskundig gezien eigenlijk in? En hoe reken je ermee? In dit artikel leggen we je alles uit over lineaire verbanden.

Wat zijn lineaire verbanden?

Een lineair verband is een relatie die continu toe- of afneemt. Dit houdt in dat bij dezelfde stapgrootte in de x-richting dezelfde hoeveelheid toe- of afneemt in de y-richting. Als de grafiek een lineaire relatie heeft, is het een rechte lijn met een bijbehorende lineaire functie. De standaardfunctie behorend bij een lineair verband is y = ax + b, waarbij a het hellingsgetal en b het startgetal (ook wel de beginwaarde genoemd) is.

Hieronder zie je de standaardgrafiek van een lineair verband:

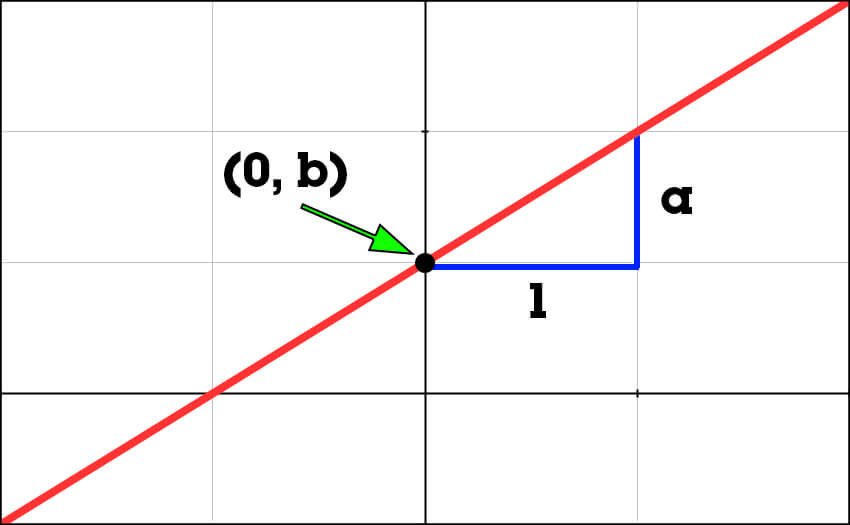
Het hellingsgetal geeft aan hoeveel eenheden de functie omhoog ofwel omlaag gaat als de x waarde 1 eenheid omhoog gaat. Het hellingsgetal wordt ook wel de richtingscoëfficiënt genoemd. Het teken voor de hellingsgetal bepaalt hierbij of de functie omhoog of omlaag gaat. Twee voorbeelden:

• Als a = -1, dan is de functie een dalende lijn, die 1 eenheid omlaag gaat als x 1 eenheid omhoog gaat.
• Als a = 1, dan is de functie een stijgende lijn, die 1 eenheid omhoog gaat als x 1 eenheid omhoog gaat.

Het startgetal geeft aan bij welke beginwaarde de functie start als x = 0. We zeggen dan ook wel dat het startgetal aangeeft waar de lijn de y-as snijdt.

Hoe reken je met lineaire verbanden?

Om met lineaire verbanden te rekenen, probeer je in eerste instantie de waarden van a (hellingsgetal) en b (startgetal) te achterhalen. Zodra je die twee hebt, kun je de formule gemakkelijk opstellen en deze invullen wanneer nodig. Het kan soms voorkomen dat één van deze twee waarden niet gegeven is. In het geval je het startgetal (b) mist, kun je x = 0 invullen en vervolgens de functie oplossen. Bij een missend hellinggetal (a) ligt het iets ingewikkelder. Als het om een lineaire functie gaat, kun je het hellinggetal berekenen met de volgende formule:

Zoals je misschien wel is opgevallen, heb je voor deze formule twee verschillende punten van de functie nodig. Stel, je weet dat (3, 9) en (10, 30) punten van de functie zijn. Het verticale verschil is dan 30 - 9 = 21, en het horizontale verschil is 10 - 3 = 7. Het hellingsgetal is dan dus 21 / 7 = 3.

Voorbeeld

Je gaat naar een kermis, waarbij de entree 5 euro is. Per attractie zijn de kosten 3 euro. Om de totale omzet van één bezoeker te berekenen, kun je de volgende formule gebruiken:

o = 3e + 5 (merk op dat dit eigenlijk y = ax + b is, maar dan met andere letters)

Hierbij is:

• o de omzet per bezoeker
• e het aantal keren in een attractie
• 3 het hellingsgetal (per 1 attractie, 3 euro omhoog)
• 5 het startgetal (0 attracties = 5 euro)

Stel dat je zou willen weten hoeveel geld je in totaal nodig zou hebben als je naar 10 attracties wil. Dat reken je als volgt uit:

o = 3e + 5

o = 3*10 + 5 = 35 euro

Hieruit blijkt dat niet elke functie een y of x hanteert. Dit is enkel de standaardfunctie. Er wordt vaak gebruikgemaakt van andere letters.

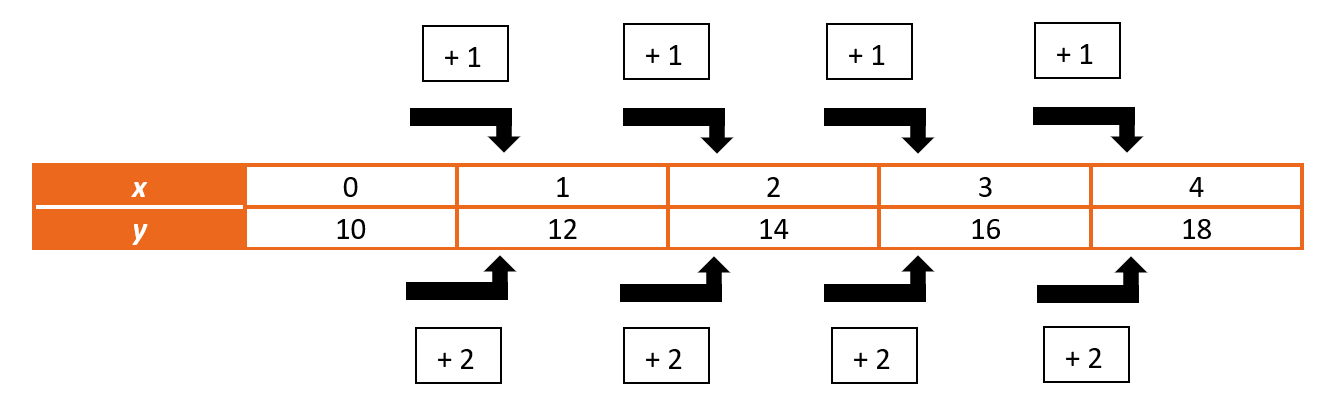
Lineair verband uit een tabel halen

Ook uit tabellen kun je lineaire verbanden herkennen. Kijk maar:

Je ziet in deze tabel dat de y-waarde steeds met 2 toeneemt als x met 1 toeneemt. Omdat er bij elke tijdstap van x dezelfde eenheidsverhoging is bij y, kan worden afgeleid dat dit gaat over een lineaire relatie. Er komt namelijk telkens hetzelfde bij. In dit geval telkens 2. Nu weten we dus dat het hellingsgetal 2 is. Dus a = 2. Om te weten wat het startgetal is, kijken we naar de beginwaarde, dus op x = 0. Dat is hier 10. Dus b = 10. Als we deze gegevens vervolgens invullen in de standaardvergelijking voor een lineair verband, komen we op de volgende functie:

y = 2x + 10

Let op: als de eerst genoteerde tabelwaarden x = -1 en y = 8 waren, dan was het startgetal dus niet 8 geweest. Het startgetal is namelijk enkel de functiewaarde behorende bij x = 0. Ook als er geen x = 0 was gegeven in de tabel, en de tabel pas begon bij x = 2, kon vanuit het hellingsgetal de functie worden afgeleid. Hierbij kon dan toch berekend worden wat het bijbehorende startgetal is.

Je kan uit de afgeleide functie ook waarden berekenen van x die niet in de tabel stonden.

Voorbeeld, stel je wilt van bovenstaande tabel weten wat de waarde van y bij is x = 120.

y = 2*120 + 10

y = 250

Dit geldt ook andersom. Bij een gegeven y-waarde kan namelijk ook de bijbehorende x-waarde worden berekend. Hierbij zit echter wel een extra tussenstap: het omschrijven van de functie.

Stel dat je zou willen weten bij welke waarde van x de waarde y = 300 is.

y = 2x + 10

y – 10 = 2x

½ y – 5 = x

½ * 300 – 5 = 145

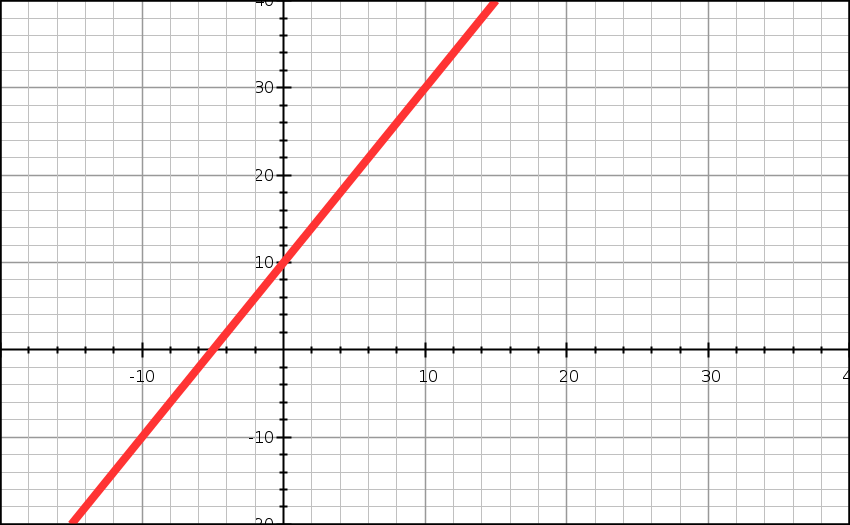
Je ziet hieronder de grafiek die hoort bij de bovenstaande tabel en de functie y = 2x + 10. Zo een grafiek kun je ook maken met de grafische rekenmachine, die je onder bepaalde voorwaarden mag gebruiken als hulpmiddel bij het examen.

Video

Deze uitlegvideo van WiskundeAcademie laat goed zien hoe je het opstellen van een lineaire formule aanpakt.