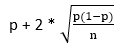Steekproeven & steekproef nemen uit een populatie

Nederland heeft ruim 17 miljoen inwoners. Om hen allemaal te ondervragen is gigantisch veel werk. Hoe weten opiniepeilers zoals Maurice de Hond vaak dan toch behoorlijk goed te voorspellen waar iedereen op gaat stemmen tijdens de verkiezingen? Dat komt omdat zij een steekproef uit de populatie nemen. Maar hoe werkt dat precies? In dit artikel lees je alles over steekproeven.

Steekproef & populatie: wat zijn het?

Een populatie is de gehele groep mensen of zaken waar je uitspraken over wilt doen. Een steekproef is een deel van de populatie dat deelneemt aan het onderzoek.

Met steekproeven willen we uitspraken doen over een populatie. Het onderzoek richt zich op een totale groep. Echter, omdat er vaak niet genoeg tijd en geld is om iedereen van de populatie te bevragen, trekken we vaak een aselecte steekproef. Met aselect bedoelen we hier 'zo willekeurig mogelijk'. Met behulp van de steekproefresultaten willen we met enige zekerheid iets zeggen over de populatie. Dit heet inferentiële statistiek.

Voorbeeld:

Laten we een voorbeeld nemen over leerlingen in een klaslokaal. We willen bijvoorbeeld weten wat de gemiddelde lengte in een klas is. De populatie is hier ‘iedereen in de klas’. We nemen allereerst een willekeurige steekproef van 3 leerlingen. We vragen wat hun lengtes (in cm) zijn. Stel dat leerling A 186 cm is, leerling B 161 cm en leerling C 195 cm. Hieruit kunnen we het gemiddelde bepalen, dat is: (186 + 161 + 195) / 3 = 180,6 cm.

Wat gebeurt er nu als we een tweede steekproef doen over 3 andere leerlingen? Leerling D is 180 cm, leerling E 169 cm en leerling F 184 cm. Het gemiddelde is nu: (180 + 169 + 184)/ 3 = 177,7 cm. We vinden dus een andere waarde. Dat komt omdat je werkt met steekproeven en niet met de populatie. Door te werken met steekproeven accepteer je dat er een afwijking van de werkelijkheid in kan zitten.

Uiteindelijk zijn we geïnteresseerd in het populatiegemiddelde, dus van iedereen die in de klas zit. Om het exacte gemiddelde van de populatie te bepalen, zou je dus van elke leerling zijn of haar lengte kunnen vragen. In een klas zou dit nog wel kunnen, maar van bijvoorbeeld de hele school wordt dit al een stuk lastiger. Omdat onderzoeken in het echt soms werken met populaties van een paar miljoen mensen, proberen we de exacte statistieken zo goed mogelijk te benaderen in plaats van ze daadwerkelijk te achterhalen.

In onderstaande tabel zijn de verschillen in kenmerken tussen een steekproef en de populatie uiteengezet.

Steekproef	Populatie
Benadering van de werkelijkheid	Werkelijkheid
Romeinse letters: x en s	Griekse letters: μ en σ
Bekend	Onbekend
Variabel	Constant
Vertellen iets over de populatie parameters	Dit willen we weten

 

 

Ook zul je de termen populatieproportie en steekproefproportie wel eens voorbij horen komen. De populatieproportie is het aantal personen met een bepaald kenmerk in een populatie ten opzichte van het totaal aantal personen in de populatie. Deze bereken je als volgt:

Populatieproportie = (aantal personen met een bepaald kenmerk in de populatie) / (totaal aantal personen in de populatie)

 

De steekproefproportie is het aantal personen met een bepaald kenmerk in een populatie ten opzichte van het totaal aantal personen in de steekproef. De formule hiervoor is:

Steekproefproportie = (aantal personen met een bepaald kenmerk in de steekproef) / (totaal aantal personen in de steekproef)

 

Bij een representatieve steekproef zal de steekproefproportie ongeveer gelijk zijn aan de populatieproportie.

Wat is het gemiddelde, de mediaan en de modus?

De drie meest bekende maatstaven uit gegevens zijn het gemiddelde, de mediaan en de modus. Deze maatstaven zie je ook duidelijk terugkomen bij de boxplot. Het gemiddelde van leerling A tot en met leerling F in bovenstaand voorbeeld is:

(186 + 161 + 195 + 180 + 169 + 184 ) / 6 = 179,2 cm.

De mediaan is de middelste waarde als de waarden geordend zijn van laag naar hoog. In bovenstaand voorbeeld is dat:

161 | 169 | 180 | 184 | 186 | 195 |

Omdat het totaal aantal gegevens even is (hier: 6, nemen we van de twee middelste waarden het gemiddelde: (180 + 184) / 2 = 182). De mediaan is hier dus 182.

De modus is de meest voorkomende waarde in de dataset. Soms is er geen waarde die het vaakst voorkomt in een dataset. In bovenstaand voorbeeld kunnen we zeggen dat elke waarde de modus is, maar ook dat er geen modus is. Stel dat we twee keer de waarde 180 cm hadden, dan was er wel een duidelijke modus geweest, namelijk 180 cm.

Maar wat nu als je een extreme waarde toevoegt aan de dataset? Bijvoorbeeld iemand van 300 cm lang. Het gemiddelde schiet dan omhoog, maar de mediaan blijft hetzelfde. Wanneer er sprake is van uitschieters (ook wel uitbijters of outliers genoemd), is de mediaan vaak het meest geschikt om de data te beschrijven. Zonder uitschieters is het gemiddelde vaak een meer geschikte maatstaf.

Waar moet je op letten bij het trekken van een steekproef?

Statistisch onderzoek zal nooit 100% kunnen aantonen dat iets waar is. Het kan echter wel aantonen dat de ene optie veel waarschijnlijker is dan de andere als er aan een aantal basisvoorwaarden voldaan is. Bij het trekken van een steekproef moet je letten op de volgende zaken:

1. Geldigheid / validiteit

   Bij geldigheid, ofwel validiteit, gaat het om de vraag: ‘weet men wat men wil weten?’ Om de validiteit te bepalen kan men de metingen voorleggen aan experts. Iedereen met didactische kennis weet dat men rekening moet houden met bepaalde zaken. Verder zal de meting verband moeten houden met andere metingen waarvan bekend is dat deze iets met het thema te maken hebben.

2. Betrouwbaarheid

   De meting moet relatief vrij van toeval-fluctuaties zijn. Onder gelijkblijvende omstandigheden dient bij een herhaalde meting de uitkomst (vrijwel) hetzelfde te zijn. De kans op onbetrouwbare metingen stijgt bijvoorbeeld als een vraag op meerdere manieren te interpreteren is.

3. Representativiteit

   Het onderzoek dient een juiste afspiegeling van de onderzoekspopulatie te tonen. Een steekproef is representatief te noemen voor de gehele populatie wanneer alle segmenten van de populatie evenredig zijn vertegenwoordigd.

4. Ontbrekende gegevens

   De ontbrekende gegevens beïnvloeden de kwaliteit van de gegevens. Denk bijvoorbeeld aan inkomen: vooral rijkeren willen hun inkomen vaak niet precies zeggen. Daardoor kunnen er grove opties van inkomens en schattingen worden uitgevoerd.

5. Aselect

   Een steekproef moet aselect zijn. Dit houdt in dat uit een populatie willekeurig personen worden gekozen om te onderzoeken. Met andere woorden: een steekproef is aselect wanneer ieder lid van de populatie een even grote kans heeft om in het onderzoek te worden meegenomen.

6. Grootte van de steekproef

   Het is de bedoeling dat we vanuit de steekproef uitspraken kunnen doen over de populatie (inferentiële statistiek). Hiervoor moet de grootte van de steekproef voldoende groot zijn. Hoe meer mensen in de steekproef, hoe beter je uitspraken kunt doen over de populatie. Met een grotere steekproef zul je ook zien dat uitschieters minder van invloed zijn op het gemiddelde.

Video

Onderstaande uitlegvideo van Math with Menno legt nog eens goed uit hoe het precies zit met het trekken van een steekproef uit een populatie.

Wat is een 95%-betrouwbaarheidsinterval en hoe bereken je het?

Een 95%-betrouwbaarheidsinterval geeft een bereik aan getallen, waarbij er een kans van 95% is dat het antwoord dat je zoekt hierin staat. Het antwoord dat je zoekt kan bijvoorbeeld het gemiddelde van de populatie zijn.

Dit interval wordt gebruikt om aan te tonen dat er een kleine kans op een fout antwoord is. Als een bepaald gegeven binnen het 95%-betrouwbaarheidsinterval valt, zeggen we ook wel dat dit antwoord significant is bij een significantieniveau van 5%. Significantie geeft aan of de resultaten te verklaren zijn door puur toeval of door de werkelijkheid. Met een 95%-betrouwbaarheidsinterval blijft er dus enkel 5% kans voor toeval over. 

Een betrouwbaarheidsinterval in statistiek gaat dus over de kans dat een populatieparameter (het werkelijke getal, dus het getal dat je probeert te benaderen) gedurende een bepaald aantal keren tussen een set waarden valt. Betrouwbaarheidsintervallen meten de mate van onzekerheid of zekerheid in een steekproefmethode. Ze kunnen een willekeurig aantal waarschijnlijkheidsgrenzen aannemen, met als meest voorkomende een betrouwbaarheidsniveau van 95%.

De linkergrens van het 95%-betrouwbaarheidsinterval voor het populatiegemiddelde bereken je als volgt:

De rechtergrens van het 95%-betrouwbaarheidsinterval voor het populatiegemiddelde bereken je als volgt:

Hierbij zijn

• X = steekproefgemiddelde
• n = omvang van de steekproef
• S = standaarddeviatie van de steekproef

Zo heb je ook de 68%-betrouwbaarheidsinterval voor de populatie. Dit ziet er misschien uit als een gek percentage, maar een steekproefverdeling van een proportie of van een gemiddelde is bij een voldoende grote steekproefomvang vaak normaal verdeeld. Zoals je misschien wel weet is 68% een belangrijke grens in de normale verdeling. De linkergrens van zo een 68%-betrouwbaarheidsinterval bereken je met:

De rechtergrens hiervan is te berekenen met:

Wanneer de steekproefproportie p en de omvang van de steekproef n bekend zijn, is het mogelijk het 95%-betrouwbaarheidsinterval voor de populatieproportie te bereken. De linkergrens bereken je dan als volgt:

Voor het berekenen van de rechtergrens gebruik je:

Video

Wil je meer weten over betrouwbaarheidsintervallen? Check dan zeker onderstaande uitlegvideo van Math with Menno.