Alles over de boxplot
Een boxplot is een grafische weergave van een dataset waarbij een minimum (laagste waarde), het eerste kwartiel, de mediaan, het derde kwartiel en een maximum (hoogste waarde) worden weergegeven. Deze dataset kan bijvoorbeeld een grote database of een steekproef uit een populatie zijn. Voordat je verder wilt gaan met de boxplot, moet je eerst weten wat deze begrippen betekenen en hoe je ze kunt berekenen. In dit artikel kun je alles lezen over de boxplot.

Video
Wil je meer weten over de boxplot? Kijk dan onderstaande video van WiskundeAcademie.
De mediaan
De mediaan is de middelste waarde van een rij getallen.
Wanneer je een oneven aantal getallen hebt, is de mediaan het middelste getal in de rij. Het middelste getal kun je als volgt vinden:
Middelste getal = (aantal getallen + 1) / 2
Voorbeeld:
We hebben de volgende getallen. 5, 5, 13, 3, 6, 9, 5, 4, 12, 5, 6, 7, 13.
We gaan deze getallen eerst op volgorde van klein naar groot zetten:
3, 4, 5, 5, 5, 5, 6, 6, 7, 9, 12, 13, 13
Dit zijn 13 getallen. Dit betekent dat het (13 + 1) / 2 = 7e getal in de rij onze mediaan is.
Het 7e getal in de rij is in dit geval 6 (3, 4, 5, 5, 5, 5, 6, 6, 7, 9, 12, 13, 13).
Wanneer je een even aantal getallen hebt, kun je geen gebruikmaken van de formule in het bovenstaande voorbeeld. Bij een even aantal getallen zit de mediaan altijd tussen de 2 middelste getallen in. De mediaan is dan het gemiddelde van deze twee middelste getallen.
Voorbeeld:
We hebben de volgende getallen: 6, 11, 9, 3, 7, 9, 4, 6.
Ook deze getallen zetten we van klein naar groot: 3, 4, 6, 6, 7, 9, 9, 11.
De mediaan zit hier tussen de 2 middelste getallen in: 3, 4, 6, 6, 7, 9, 9, 11.
De mediaan is dan (6 + 7) / 2 = 6,5.
Eerste en derde kwartiel

Nu we de mediaan hebben, zouden we ook de kwartielen kunnen berekenen. De mediaan splitst de rij getallen als het ware in twee stukken. Hierdoor heb je een linkergedeelte en een rechtergedeelte. Het eerste kwartiel is als het ware de mediaan van het linkergedeelte. Deze kun je bepalen op dezelfde manier als hierboven uitgelegd. Het derde kwartiel is de mediaan van het rechtergedeelte.
Voorbeeld:
3, 4, 6, 6, 7, 9, 9, 11
Dit is een even aantal getallen. De mediaan zit hier dan tussen de 2 middelste getallen in: 3, 4, 6, 6, 7, 9, 9, 11. De mediaan is dan (6 + 7) / 2 = 6,5.
Om het eerste kwartiel te bepalen, splits je de getallen in 2 delen.
Het eerste kwartiel valt in het linkergedeelte en het derde kwartiel in het rechtergedeelte.
3, 4, 6, 6, | 7, 9, 9, 11
Links Rechts
Het eerste kwartiel bevindt zich tussen de 4 en 6 in. Het eerste kwartiel is dan (4 + 6) / 2 = 5.
Het derde kwartiel bevindt zich tussen de 9 en de 9 in. Het derde kwartiel is dan (9 + 9) / 2 = 9.
De boxplot

Nu we weten wat de mediaan, het eerste kwartiel en het derde kwartiel betekenen, kunnen we een boxplot gaan tekenen. In een boxplot gaan we verder gebruikmaken van het minimum (de laagste waarde) en het maximum (de hoogste waarde).
Een boxplot maak je als volgt. Maak eerst de betreffende getallenlijn. Zet daarna een stip boven de getallenlijn ter hoogte van de laagste waarde, het eerste kwartiel, de mediaan, het derde kwartiel en de hoogste waarde. Vervolgens teken je een rechthoek tussen kwartiel 1 en kwartiel 3 en zet je een streep bij de mediaan (zie de afbeelding hieronder). Nu heb je een boxplot getekend.
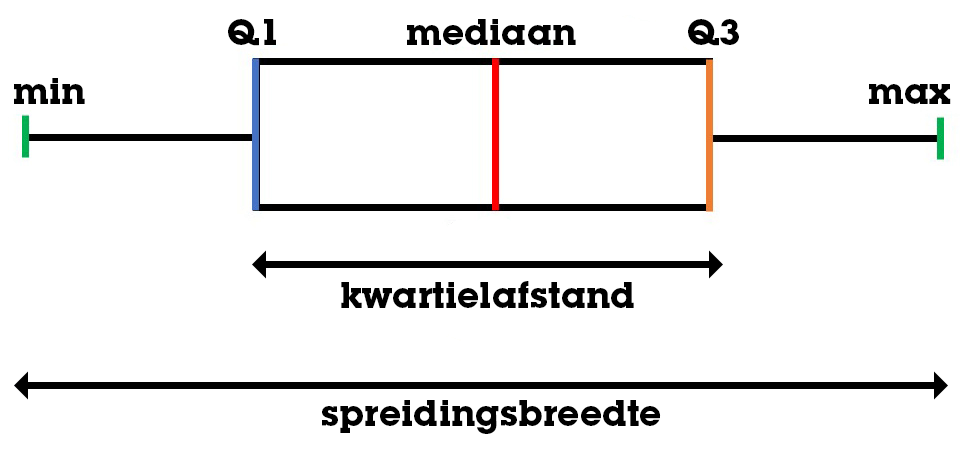
De spreidingsbreedte is het verschil tussen het grootste en kleinste waarnemingsgetal. Deze bereken je als volgt: de hoogste waarde – de laagste waarde.
De kwartielafstand is het verschil tussen het derde en eerste kwartiel. Deze bereken je als volgt: derde kwartiel – eerste kwartiel.
Wil je zelf een boxplot kunnen tekenen? Volg dan de stappen uit onderstaande video.
Deel dit artikel
-
-
-
-
-
-
-
- Kies je niveau
- Kies je producten
- Kies je vakken
Voordeelpakket
Tot 21% stapelkorting!
-
-
-
-
-
-
-
- Kies je niveau
- Kies je producten
- Kies je vakken
Voordeelpakket
Tot 21% stapelkorting!
-
Ontvang exclusieve tips in het examenjaar
Graag helpen we jou in het examenjaar richting je diploma!
Zit jij in je examenjaar en wil jij slagen? Schrijf je dan in voor:
Exclusieve tips
De geheimen van het eindexamen
Een template voor jouw leerplanning
Dat extra zetje in de rug














