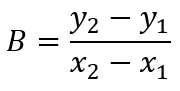Interpoleren en extrapoleren
Interpoleren en extrapoleren is iets dat je veel zal tegenkomen tijdens het doen van onderzoek of het uitvoeren van proefjes. Soms wil je namelijk iets zeggen over waarden die niet volledig bekend zijn. Je kunt deze gegevens dan soms 'schatten'. Je zou interpoleren en extrapoleren kunnen zien als een wiskundige manier van schatten. Hoe dit precies werkt, gaan we je in dit artikel uitleggen.
Verschil tussen intrapoleren en extrapoleren
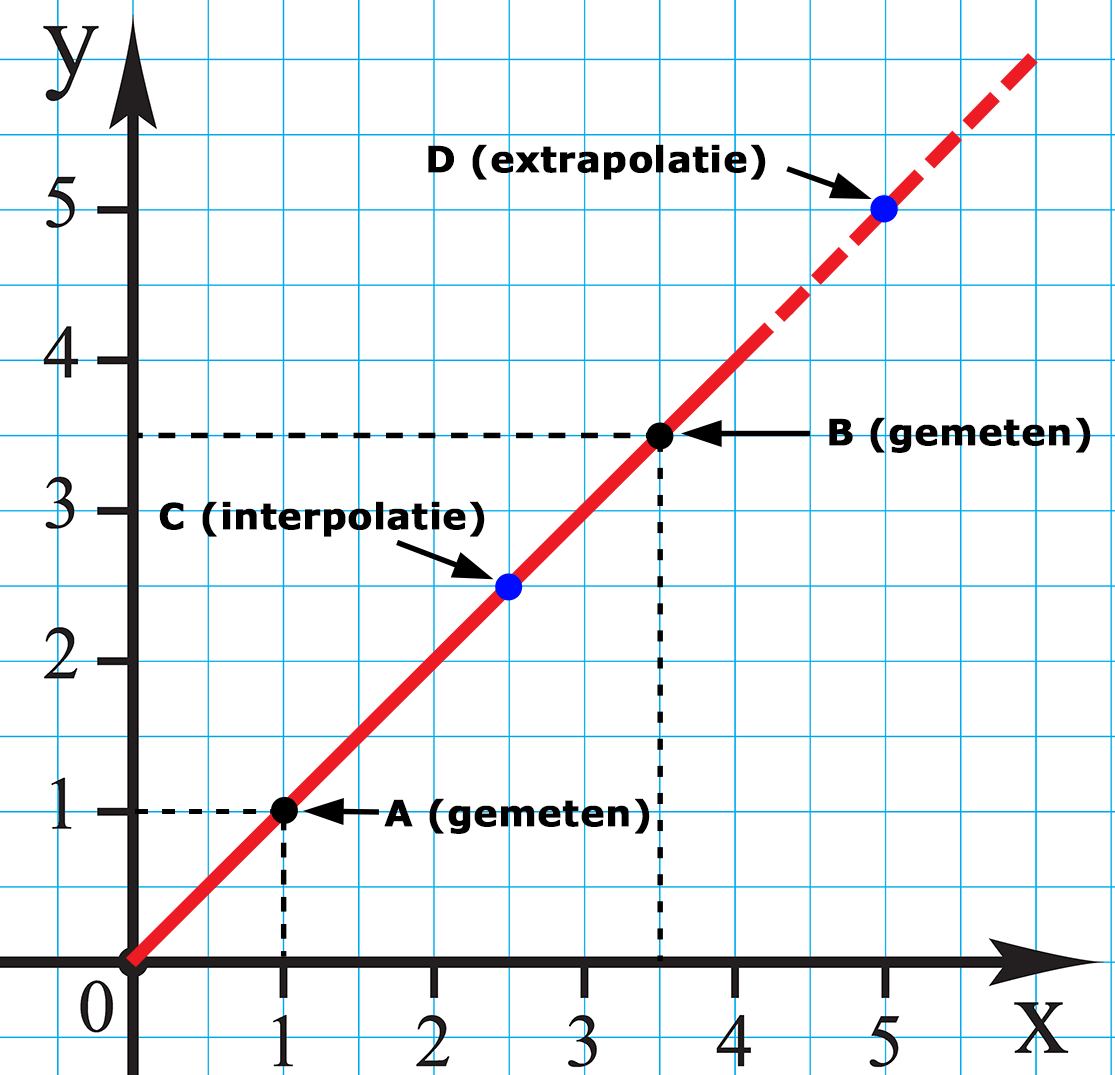
Bij interpoleren gaat het om schatten van een waarde die binnen de gegevens ligt, en bij extrapoleren ligt de waarde die je wilt schatten buiten de beschikbare gegevens. De afbeelding hieronder laat het verschil tussen interpoleren en extrapoleren zien.
Interpoleren
Interpoleren is het schatten van waarden die tussen twee beschikbare waarden liggen. De meest voorkomende manier is lineaire interpolatie. Dat werkt als volgt.
Stel dat de volgende tabel het brandstofverbruik van auto's geeft:
| Snelheid (km/u) | Brandstofverbruik (L/100km) |
|---|---|
| 10 | 18.1 |
| 20 | 11.8 |
| 30 | 9.8 |
| 40 | 8.6 |
| 50 | 8.1 |
Als we het brandstofverbruik op een snelheid van 27 km/u willen weten, kunnen we dat niet achterhalen uit deze tabel van beschikbare gegevens. Wat we wel kunnen doen, is lineair interpoleren. We nemen dan aan dat de relatie tussen snelheid en brandstofverbruik lineair is om zo de vereiste gegevens te bepalen.
De algemene formule voor een lineaire interpolatie tussen twee beschikbare gegevens is:
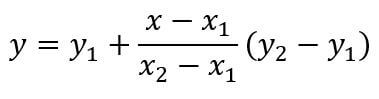
Hierbij is:
- y de gezochte waarde van de afhankelijke variabele
- x de waarde van de onafhankelijke variabele
- x₁ de beschikbare waarde van de onafhankelijke variabele kleiner dan x
- x₂ de beschikbare waarde van de onafhankelijke variabele groter dan x
- y₁ de beschikbare waarde van de afhankelijke variabele bij x₁
- y₂ de beschikbare waarde van de afhankelijke variabele bij x₂
In ons voorbeeld van brandstofverbruik B bij 27 km/u, zou het dus de volgende vergelijking opleveren:
B = 11,8 + (9,8 - 11,8) × (27 - 20) / (30 - 20) = 10,4 L/100 km.
Uit de brandstofverbruikstabel is af te leiden dat er geen directe lineaire relatie is tussen verbruik en snelheid: het verbruik van 10 km/u naar 20 km/u daalt met 6,3 L/100 km, terwijl het verbruik van 40 km/u naar 50 km/u slechts 0,5 liter/100 km is. In feite is lineaire interpolatie dus niet helemaal redelijk.
Het is echter belangrijk om de volgende punten in overweging te nemen:
- Lineaire interpolatie zal grotere fouten opleveren op het moment dat het sterkere niet-lineaire functies betreft.
- De fout is het kleinst bij de tabelwaarde van x (in dit voorbeeld dus ongeveer 10 km/u, 20 km/u, etc.) en het grootst in het midden (in dit voorbeeld dus ongeveer 15 km/u, 25 km/u, etc.).
Extrapoleren
Extrapoleren is het schatten van een waarde die buiten het bereik van een set gegevens valt. Hierbij wordt er verondersteld dat er een bepaalde relatie tussen de gegevens bestaat. Je kunt bijvoorbeeld extrapoleren omdat er gedurende een bepaalde tijd geen meetresultaten zijn, of omdat je een toekomstige waarde wilt weten.
Extrapoleren is 'gevaarlijker' dan interpoleren, omdat de gegevens zich buiten het bekende gebied bevinden. Het is dus minder betrouwbaar. Veel hangt af van de veronderstelde relatie tussen de gegevens, zoals een lineaire of exponentiële relatie.
Omdat extrapoleren dus meer onzekerheid met zich meebrengt, moet er bij de extrapolatiemethode altijd aangegeven worden hoe de nieuwe gegevens kunnen worden verkregen. Zo zou je bijvoorbeeld kunnen zeggen: “De hoeveelheid coronabesmettingen voor de komende 2 weken is afgeleid op grond van extrapoleren van de gegevens van september 2020”.
Extrapoleren en voorspellen gaan hand in hand. Daarom maakt bijna elk vakgebied dat gaat over verwachtingen over de toekomst, gebruik van extrapolatie.
Ook de extrapolatiemethoden kunnen we uitvoeren. We nemen hiervoor hetzelfde voorbeeld met dezelfde gegevens als bij het interpoleren, namelijk over het brandstofverbruik. Stel dat we zouden willen weten wat het brandstofverbruik is bij een snelheid van 60 km/u. We kunnen dit immers niet aflezen uit de tabel, aangezien het buiten het bereik van de gegevens valt. Het beste wat hierbij gedaan kan worden is de hoogst beschikbare gegevens gebruiken. Die geven namelijk de laatste trend van de grafiek weer.
| Snelheid (km/u) | Brandstofverbruik (L/100km) |
|---|---|
| 10 | 18.1 |
| 20 | 11.8 |
| 30 | 9.8 |
| 40 | 8.6 |
| 50 | 8.1 |
Van de snelheid tussen 40km/u en 50km/u wordt de helling bepaald. We gebruiken daarvoor de volgende formule:
B = (8.1 - 8.6) / (50 – 40) = (-0,5)/(10) = -0,05
Vervolgens vullen we de waarde van B in in de volgende formule:
y = Bx + 8,1
y = -0,05*60 + 8,1
y = 5,1 L/100 km
Dus het brandstofverbruik bij 60km/u zou 5,1L/100km zijn.
Video
Wil je meer uitleg en voorbeelden over interpoleren en extrapoleren? Check dan onderstaande video van WiskundeAcademie.
