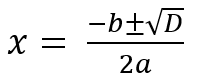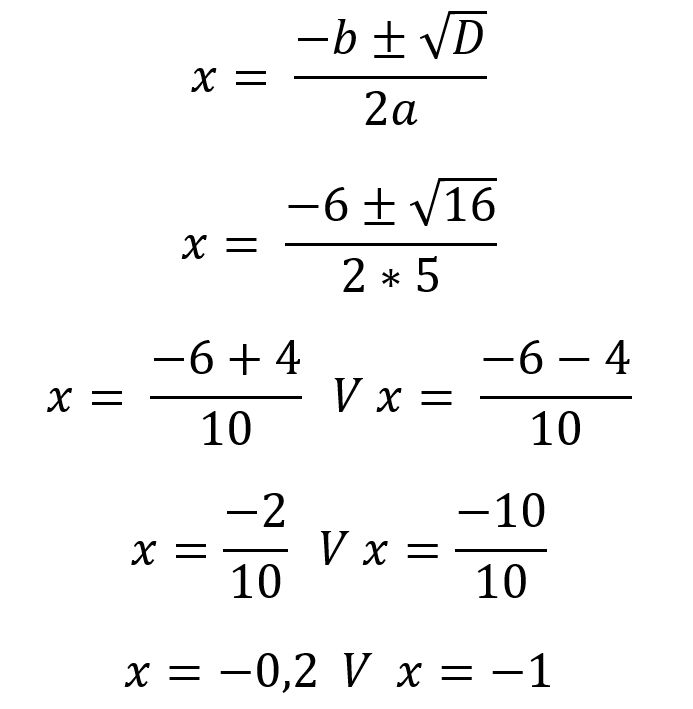ABC-formule

Zoals je in groep 3 'het ABC' hebt moeten leren, moet je op de middelbare school de ABC-formule leren. Net zoals met 'het abc' lijkt de abc-formule in het begin erg lastig. Maar als je eenmaal begint met oefenen, zul je merken dat het eigenlijk best wel goed te doen is. Uiteindelijk is het een kwestie van aflezen, invullen en uitrekenen. In dit artikel leggen we je alles uit over de ABC-formule en laten we je zien hoe je ermee rekent.

Wat is de ABC-formule?

De ABC-formule is een formule die je gebruikt om een kwadratische vergelijking op te lossen. De formule ziet er als volgt uit:

 

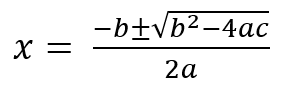
of

 

Een kwadratische vergelijking is een vergelijking met daarin een kwadraat van de variabele. Vaak noemen we die variabele 'x'. De ABC-formule, ook wel de wortelformule genoemd, kan altijd worden gebruikt om kwadratische vergelijkingen op te lossen, maar soms kun je een kwadratische vergelijking makkelijker ontbinden in factoren. Als je ziet hoe je hem kan ontbinden in factoren moet je dat vooral doen, maar staar er niet te lang naar. Dat is zonde van je tijd. De ABC-formule werkt gegarandeerd.

Hoe gebruik je de ABC-formule?

Stap 1: aflezen

Oké, we hebben besloten om een kwadratische vergelijking op te lossen met de ABC-formule. Deze vergelijking kan er in het begin moeilijk uitzien. Daarom schrijven we hem eerst om naar de volgende standaardvorm:

a × x² + b × x + c = 0

Hier is x de variabele en zijn a, b en c de constanten. Echter, om deze simpele vorm te bereiken moet je waarschijnlijk een beetje schuiven. Schrijf daarom eerst de vergelijking op waar je mee begint. Werk vervolgens (stapsgewijs) naar de standaardvorm toe. Doe dit zorgvuldig, want een plus/min-fout is snel gemaakt.

Let op: Het is mogelijk dat b en/of c een waarde heeft van 0. Dat mag, zolang a maar een waarde heeft anders dan 0. Als a = 0 dan valt het kwadraat namelijk weg en dan heet het geen kwadratische vergelijking meer. Hieronder een voorbeeld:

3x² + 2 = 0 geeft ons a = 3, b = 0, c = 2

4x + 5 = 0 is géén kwadratische vergelijking

Tip: Schrijf de waarden voor a, b en c tussen haakjes op als ze uit meerdere componenten bestaan. Zo voorkom je dat je er één vergeet bij het invullen in de ABC-formule. In het voorbeeld hieronder is de waarde voor c gelijk aan (18 - p). Later zullen we terugkomen op constante parameters zoals p. Zonder haakjes kun je p over het hoofd zien of hem in het rechterlid plaatsen en in de war raken. Voorbeeld:

4x² + 15x + (18 - p) = 0

Tip: Als je het moeilijk vindt om overzicht te bewaren, kun je de a, b en c nog een keer los voor jezelf opschrijven nadat je de vergelijking hebt omgeschreven. Zo voorkom je afleesfouten. Het vorige voorbeeld levert de volgende waarden op:

a = 4

b = 15

c = 18 - p

Stap 2: invullen

We hebben de waarden voor a, b en c gevonden. Nu kunnen we de ABC-formule invullen. Deze ziet er als volgt uit:

       

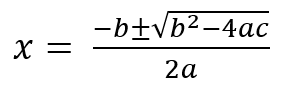
of 

 

In principe kun je gewoon de waarden van a, b en c invullen en zo x vinden. Maar hé, waarom hebben we twee versies van de ABC-formule? In de onderste versie is namelijk alles onder de wortel vervangen door een D. Voordat we de formule gaan invullen, moeten we het even hebben over die D.

De D staat voor discriminant. Je kunt de discriminant ook schrijven als D = b² - 4ac. Waarom verzinnen we dan een extra letter? We kunnen toch ook gewoon de linker ABC-formule direct invullen? Dat doen we omdat dit stukje van de formule extra belangrijk is. Want als we deze eerst los uitrekenen, komen we erachter hoeveel oplossingen onze kwadratische vergelijking heeft. Vul a, b en c in om een waarde voor D te krijgen.

Voorbeeld:

5x² + 6x +1 = 0

a = 5, b = 6, c =1

D = b² - 4ac

D = 6² - 4 × 5 × 1

36 - 20 = 16

D is uitgerekend, maar wat betekent dit nu eigenlijk? Om daarachter te komen, kijken we in het onderstaande lijstje.

D < 0 betekent dat de vergelijking geen oplossingen heeft

D = 0 betekent dat de vergelijking één oplossing heeft

D > 0 betekent dat de vergelijking twee oplossingen heeft

Dit lijstje heb je vast al wel vaker voorbij zien komen, maar waarom is dit zo? Dat is heel simpel. Laten we nog even kijken naar de volledige ABC-formule. De D staat onder een wortelteken. Wat gebeurt er als je de wortel wilt nemen van een negatief getal? Precies ja, dat kan niet. Daarom zijn er 0 oplossingen als D een negatief getal is. Als D gelijk is aan 0, valt de hele wortelterm weg. Je houdt dan over dat 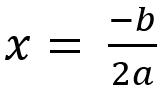. Dat geeft één oplossing. Als D groter is dan 0 (dat is dus een positief getal), komen er wél oplossingen uit.

Het voorbeeld gaf ons D = 16. Dat betekent dat de kwadratische vergelijking 5x² + 6x + 1 = 0 twee oplossingen heeft.

Fun fact: De ABC-formule wordt ook wel geschreven met een ± teken in het midden. Dit teken staat daar omdat de wortel van een positief getal altijd twee oplossingen heeft: een positieve en een negatieve. Kijk maar naar dit voorbeeld:

2² = 4

(-2)² = 4

√4 = 2 V √4 = -2

Eigenlijk zou je de ABC-formule dus ook kunnen schrijven met een + in plaats van een ±, maar we schrijven de ± als ezelsbruggetje voor onszelf. De V is trouwens een wiskundige notatie voor “of”.

Het is dus nuttig om D eerst uit te rekenen, maar je mag hem ook vervangen door (b² - 4ac) in de ABC-formule. Werk dan wel extra zorgvuldig.

Stap 3: uitrekenen

Je hebt nu alle waarden ingevuld in de formule en hopelijk de discriminant uitgerekend. Het is tijd voor het uitrekenen. Na het invullen van a, b, c en D, gaan we de formule uitwerken om één of meerdere oplossingen voor x te vinden. Werk zorgvuldig en gebruik tussenstappen. Hou rekening met de juiste volgorde. Als je dat moeilijk vindt, kijk dan nog even hoe je precies haakjes wegwerkt.

Na het uitwerken krijg je, als er een antwoord is, één of meerdere oplossingen voor x. De kwadratische vergelijking is opgelost. Het voorbeeld uit de vorige stap van 5x² + 6x + 1 = 0 levert ons het volgende op:

Wat doe je als er extra parameters voorkomen?

Het kan voorkomen dat je naast x nóg een onbekende in je vergelijking hebt. Deze extra onbekende noemen we een parameter en heeft vaak een naam als p of q, maar het kan in theorie natuurlijk elke naam hebben. Een parameter kan voorkomen bij vragen als: "voor welke waarde van p heeft deze vergelijking twee oplossingen?" Dan moeten bij jou de alarmbellen afgaan: twee oplossingen? Dat betekent dat D > 0!  Vul (b² - 4ac) > 0  in en werk dit uit tot een stelling voor p.

Voorbeeld

Voor welke waarde van p heeft x² + 4x - 2 + p = 1 twee oplossingen?

x² + 4x - 3 + p = 0

a = 1, b = 4, c = p -3

D > 0, dus (b² - 4ac) > 0

(4² - 4 × 1 × (p - 3)) > 0

(16 - 4p + 12) > 0

(28 - 4p) > 0

-4p > -28

p < (-28 / -4)

p < 7

Dus voor elke waarde van p kleiner dan 7 geeft de kwadratische vergelijking x² + 4x - 2 + p = 1 twee oplossingen.

Dit soort vragen zie je vaak bij sommen waarbij twee of meer functies elkaar tegenkomen. Ook als je de woorden snijpunt of raakpunt tegenkomt in je vraag, moeten de alarmbellen af gaan. Het is fijn om de grafiek dan te visualiseren. Dan kun je je wat voorstellen bij die 0, 1 of 2 oplossingen.

Video

Wil je een video zien waar de ABC-formule stap voor stap wordt uitgelegd en toegepast? Check dan deze uitlegvideo van WiskundeAcademie.