Wortelverbanden

Wortels zijn natuurlijk gezond en lekker om te eten, maar wortels zijn ook een belangrijk onderdeel in de wiskunde. In dit artikel lees je meer over wortelverbanden en leer je hoe je met wortels rekent.

Wat is een vierkantswortel?

Een vierkantswortel is het tegenovergestelde van een kwadraat. Het nemen van een vierkantswortel van een getal is dan ook het tegenovergestelde van het kwadraat nemen van een getal. Zo is 3 in het kwadraat bijvoorbeeld 9 (3² = 9), dus de vierkantswortel van 9 is 3. In symbolen is dit √9 = 3. Het "√" -symbool laat hier zien dat je te maken hebt met een vierkantswortel. Vierkantswortels zijn de bekendste soort wortels. Deze vierkantswortel kun je op de meeste rekenmachines vinden, zeker op de grafische rekenmachines die je tijdens het eindexamen mag gebruiken.

Vergeet hierbij niet dat elk getal eigenlijk twee vierkantswortels heeft. Voorbeeld: 3 vermenigvuldigd met 3 is gelijk aan negen (3² = 9) maar -3 vermenigvuldigd met -3 is ook gelijk aan negen (-3)² = 9. Met andere woorden: 3² = (−3)² = 9, maar ook √9 = ± 3, waarbij de ± staat voor 'plus of min'.

Vierkantswortels vereenvoudigen

Hetgeen wat een belangrijke vaardigheid is en vaak als moeilijk wordt ervaren is het vereenvoudigen van vierkantswortels. Echter, je hoeft maar enkele eenvoudige regels te onthouden om dit soort problemen op te lossen. Vierkantswortels kunnen namelijk op dezelfde manier worden ontbonden als gewone getallen. Kijk maar: 6 = 2 × 3, dus √6 = √2 × √3. Houd dus ook altijd de algemene voorrangsregels in de wiskunde in het achterhoofd.

Nu was het voorbeeld hierboven makkelijk, maar het kan natuurlijk ook voorkomen dat je met grotere getallen te maken krijgt. Het vereenvoudigen van grotere wortels, is het makkelijkst als je de wortel stap voor stap factoriseert.

Neem bijvoorbeeld √132. √132 is een grote wortel en het kan moeilijk te zien zijn wat je precies moet doen. Je kunt echter wel snel zien dat het getal deelbaar is door 2, dus je kunt √132 = √2 × √66 schrijven. Het getal 66 is echter ook deelbaar door 2, dus heb je nu: √2 × √66 = √2 × √2 × √33. In dit geval geeft een vierkantswortel van een getal vermenigvuldigd met een andere vierkantswortel (√2 × √2) het oorspronkelijke getal (dit is immers de betekenis van de vierkantswortel). Daarom geldt √132 = √2 × √2 × √33 = 2 × √33.

Kortom, kun je de vierkantswortels vereenvoudigen met behulp van de volgende regels:

• √ (a × b) = √a × √b
• √a × √a = a

Maar wat is dan de wortel van een negatief getal? Hiervoor is ook een oplossing! Die oplossing is namelijk het getal van i, ook wel imaginaire getal. Je hoeft dat niet te kennen voor het eindexamen, maar als je het interessant vindt kun je het eens online opzoeken.

Voorbeeld

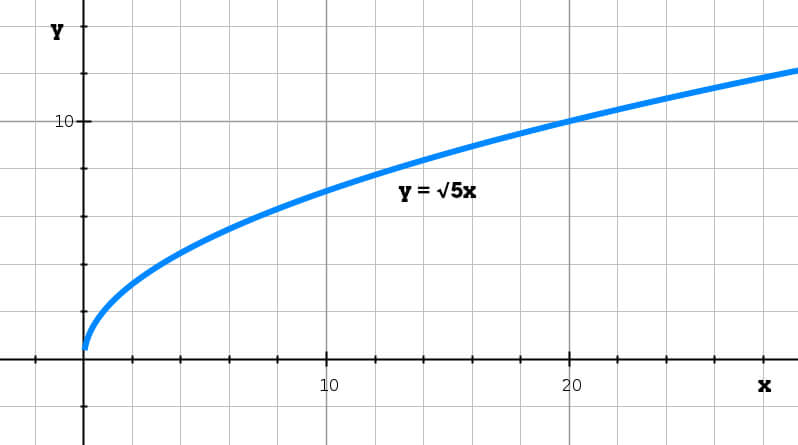
Neem de formule y = √5x en zie onderstaande tabel.

x	y
0	0
1	2,24
2	3,16
3	3,87
4	4,47
5	5
6	5,48
7	5,92

Als x = 0, geldt dat ook y = 0 is. Dit is duidelijk, omdat alles vermenigvuldigd met 0, ook 0 oplevert, en dit geldt ook voor wortels. Bij x = 5, geldt y = 5. Je vermenigvuldigt namelijk het getal 5 met zichzelf en je ziet dat je de wortel ervan moet nemen, wat dan dus 5 is. Door al de waarden van x in te vullen in de vergelijking, kunnen de waarden van y verkregen worden. Hieruit is het weer mogelijk om een grafiek te maken, door de verkregen coördinaten als een lijn met elkaar te verbinden. Die grafiek komt er dan als volgt uit te zien:

Voorbeelden van rekenen met wortels

• √12 = √2 × √6 = √2 × √2 × √3 = 2 × √3 = 3,4641
• √24 = √2 × √12 = √2 × √2 × √6 = 2 × √6 = 4,8990
• √36 = √2 × √18 = √2 × √2 × √9 = 2 × √9 = 2 × 3 = 12
• √72 = √2 × √36 = √2 × √4 × √9 = √2 × √2 × √2 × √9 = 2 × √2 × √9 = 6 × √2 = 8,4853

Andere wortels

Het komt ook wel eens voor dat je te maken hebt met een kubuswortel, oftewel een derdemachtswortel van een getal. Net als vierkantswortels zijn deze precies het tegenovergestelde van de macht van getallen. Dus 3³ = 27, en dat betekent dat de kubuswortel van 27^1/3 is, ofwel ∛27 = 3. Het symbool "∛" vertegenwoordigt de kubuswortel van het getal dat erna komt.

Wortels worden soms ook uitgedrukt als fractionele machten, dus √x = x^1/2 en ∛x = x^1/3.

Video

Wil je meer weten over het oplossen van wortelvergelijkingen? Bekijk dan deze uitlegvideo van WiskundeAcademie: