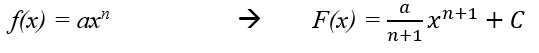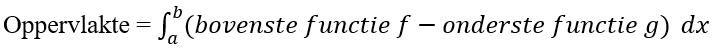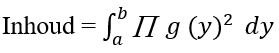Integralen berekenen
Je herinnert je vast alle oppervlakte-oefeningen uit je wiskunde huiswerk van vroeger nog wel: van 'hoeveel vierkante meter is deze tuin?' tot aan 'bereken de oppervlakte van deze driehoek'. Deze oefeningen gingen vaak over het berekenen van vrij eenvoudige figuren. Appeltje-eitje! Maar wat nou als het figuur een nogal vreemde vorm heeft? Dan gebruik je integralen! In dit artikel leggen we je alles uit over integraalrekening.
Wat is de integraalrekening?

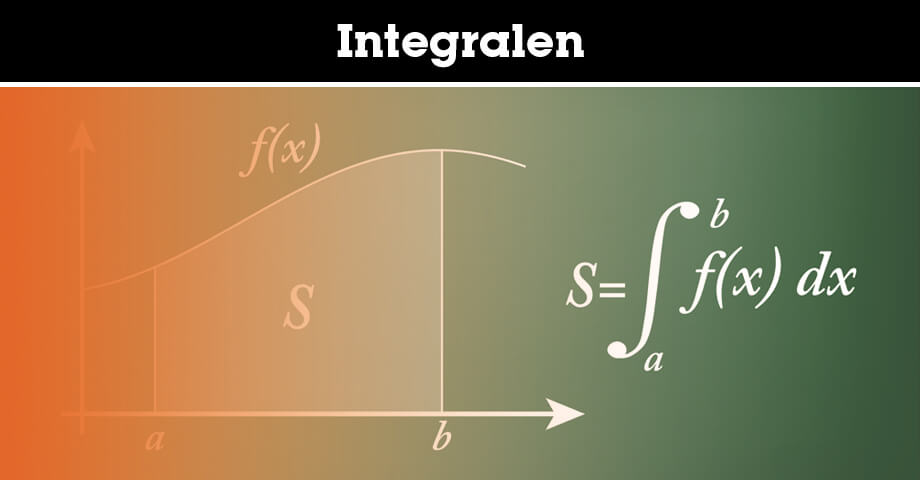
De integraalrekening is een berekening die wordt gebruikt om onder andere de oppervlakte onder een grafiek te vinden. De integraal die hiervoor gebruikt wordt, ziet er als volgt uit:
Als je bezig bent met het berekenen van integralen, ben je bezig met primitiveren. Primitiveren is het omgekeerde van differentiëren.
- Als er wordt gedifferentieerd, zoek je de eerste afgeleide functie f’(x) van de oorspronkelijke functie f(x);
- Als er wordt geprimitiveerd, zoek je de primitieve functie F(x) van de oorspronkelijke functie f(x).
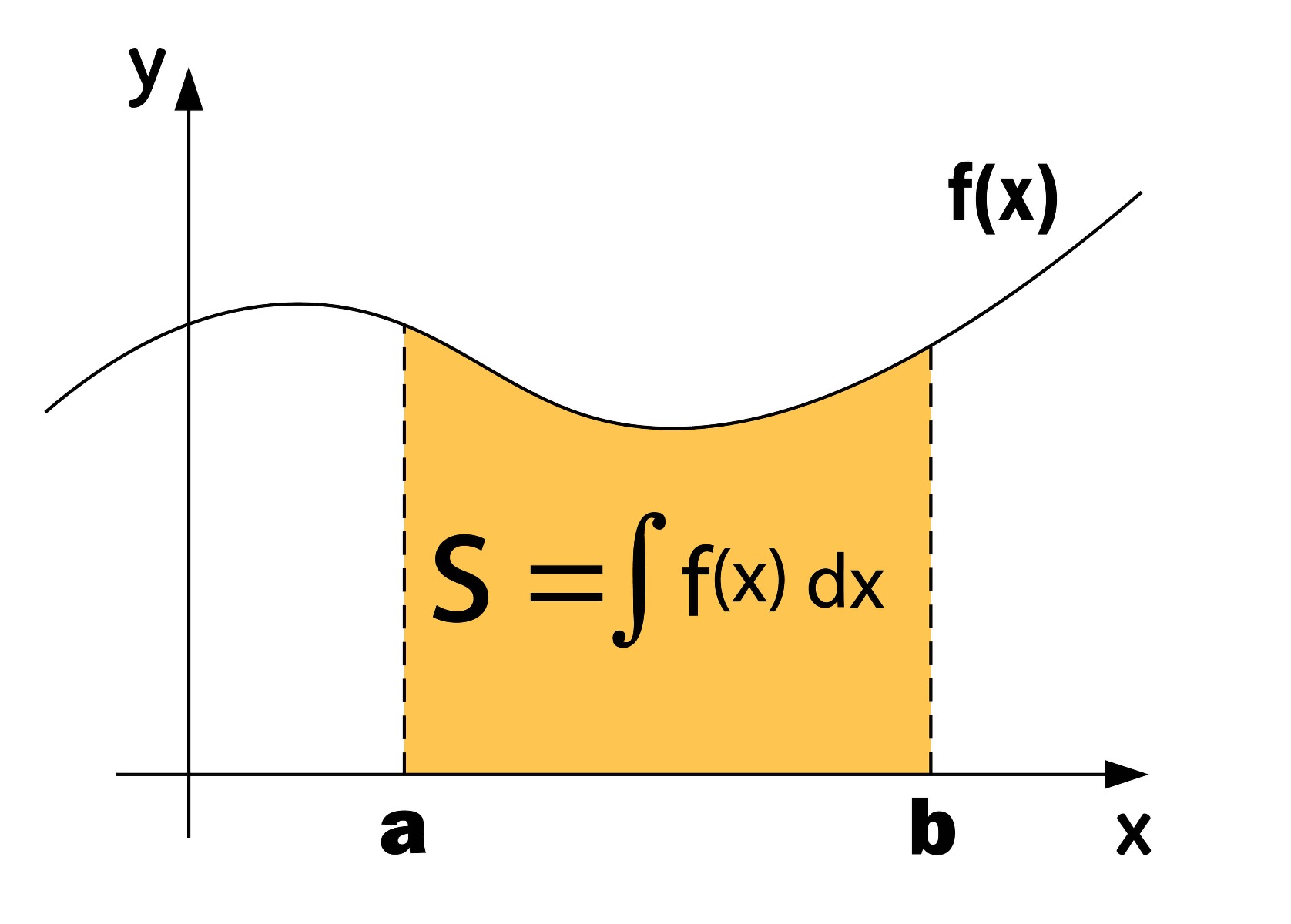
In de afbeelding hieronder is de grafiek te zien van een functie f(x). Hierbij is er een gebied S, waarvan we de oppervlakte willen berekenen. Je weet vast nog wel hoe je de oppervlakte van reguliere geometrische lichamen kunnen berekenen, maar het lijkt er in dit geval op dat er meer informatie nodig is om de oppervlakte S te berekenen. Aan het eind van dit artikel wordt duidelijk hoe we dit probleem wiskundig kunnen oplossen.
Om zulke berekeningen uit te voeren is het van belang om naast de standaard voorrangsregels in de wiskunde ook de basisregels van primitiveren paraat te hebben:
Hieruit volgen drie zaken waar je op moet letten:
- Bij het primitiveren van de 6e basisregel
krijg je absolute waardestrepen. Dit houdt in dat de waarde niet negatief kan worden. In veel vakken, zoals natuurkunde, zul je nog wel eens tegenkomen dat deze vaak vergeten worden en er gebogen haakjes gebruikt worden. Dit komt doordat in de natuurkunde er haast geen sprake is van negatieve waarde. Echter, de absolute waardestrepen zijn wiskundig gezien wel degelijk de juiste notatievorm.
- Bovendien moet je ook de +C niet vergeten bij het integreren. Dit wordt ook wel de integratieconstante genoemd. Je kan niet weten welk getal het precies zou moeten zijn, waardoor de C wordt genoteerd.
- Bij het differentiëren werd veelvuldig gebruikgemaakt van de kettingregel. Uit basisregel 1 luidt dat bij het primitiveren een omgekeerde bewerking wordt uitgevoerd. De macht n wordt namelijk +1 hoger, en je vermenigvuldigt de macht n niet meer, maar je deelt juist de macht n+1 met de ‘x’:
Wat is de Riemann-som?
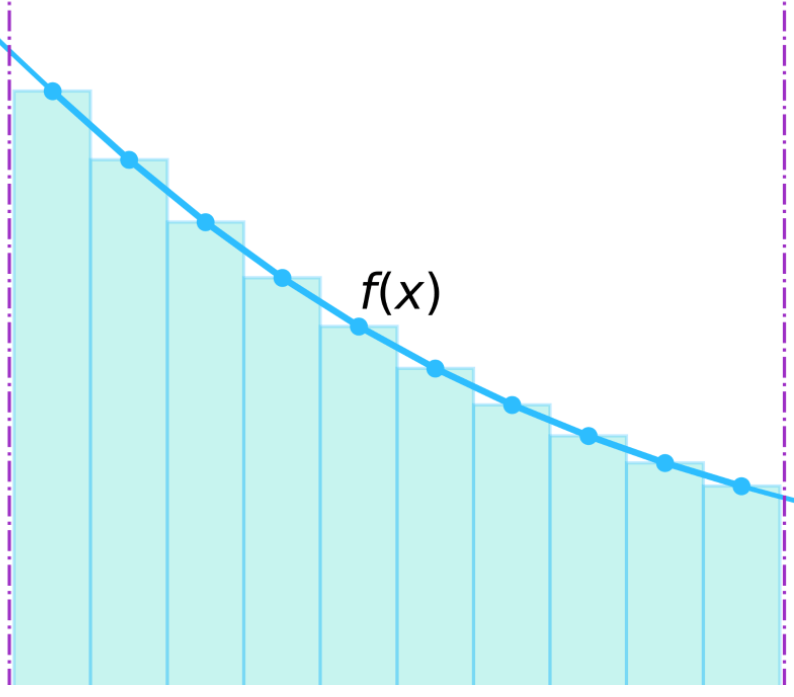
De Riemann-som is een manier om niet-standaard oppervlaktes te berekenen waarbij de oppervlaktes worden verdeeld in rechthoeken. Op die manier kun je de uiteindelijke oppervlakte toch redelijk goed benaderen. Theoretisch kan deze methode vrijwel nooit worden toegepast, maar voor veel praktische zaken is het erg handig. De Riemann-som is vernoemd naar de ontdekker van deze methode Bernhard Riemann. Een voorbeeld van een Riemann-som zie je in de volgende figuur:
Bron: Isquared
Het is je misschien wel opgevallen dat er gaten zijn in het gebied in de rechthoektekening en dat het gebied dat je uiteindelijk berekent kleiner is dan het werkelijke gebied van S. Naarmate het aantal rechthoeken toeneemt, worden de gaten in het S-veld kleiner. Dit betekent dat hoe meer rechthoeken we tekenen, hoe dichter we bij de echte waarde van het oppervlak komen.
Het vergt natuurlijk te veel tijd om dit rechthoek voor rechthoek te tekenen. Het kan veel gemakkelijker én sneller door het op te lossen met de wiskundige technieken.
Het gebied S bevindt zich onder de functiecurve f(x), de x-as en de grenzen a en b. Met de primitieve F(x) kunnen we de oppervlakte S wiskundig berekenen. De integraal wordt als volgt genoteerd:
De waarde b bovenin de integraalteken is de bovengrens, en de waarde a onderin de integraalteken is de ondergrens. De dx geeft aan dat het een integratie-variabele is in de functie. Het berekenen van deze integraal noemen we integreren.
Hoe bereken je de oppervlakte tussen twee grafieken?
De formule om de oppervlakte tussen twee grafieken te berekenen, is de volgende standaardformule:
Deze formule geldt te allen tijde. Het maakt niet uit of de grafieken deels of helemaal boven of onder de x-as liggen. Het addertje onder het gras komt pas wanneer je het oppervlak moet berekenen tussen de grafiek en de x-as. De waarde van het oppervlak onder de x-as komt dan namelijk negatief uit. Hetgeen wat je dan moet doen is de absolute waarde van de functie nemen, dus:
Hoe bereken je de inhoud van een functie die om de x-as wentelt?
Het komt ook veelvuldig voor dat een functie om de x-as wentelt. Je bent dan niet meer op zoek naar het tweedimensionale oppervlak, maar naar de driedimensionale inhoud. Dit noemen we ook wel het omwentelingslichaam. De standaardformule luidt als volgt:
De constante kan uiteraard ook naar buiten gehaald worden. Dit maakt het berekenen gemakkelijker.
De 
Hoe bereken je de inhoud van een functie die om de y-as wentelt?
Net zoals we kunnen omwentelen om de x-as, kunnen we ook omwentelen om de y-as.
Om de inhoud van een omwentelingslichaam te vinden bij een omwenteling om de y-as, wordt de volgende formule gebruikt:
Let er hierbij op dat er nu geen sprake is van dx, maar dy.
In onderstaand figuur is links de ongelimiteerde integraalteken te zien en rechts het somteken. Het integrale symbool is een licht gewijzigd somteken. De reden hiervoor heeft te maken met de mate waarin de Integraal betrekking heeft op het "totaal", de som van de rechthoeken.
Overige informatie over de integraal
Het is goed om te weten dat de integraal op veel verschillende manieren kan worden beschreven, vereenvoudigd of moeilijker gemaakt. Verder is het belangrijk om de functie f en F niet door elkaar te halen. De functie F is immers de primitieve van de functie f. Met andere woorden: de afgeleide van de functie F is f.
Wil je alles over het berekenen van integralen nog eens uitgelegd hebben in beeld en geluid? Check dan deze video van WiskundeAcademie!

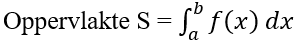
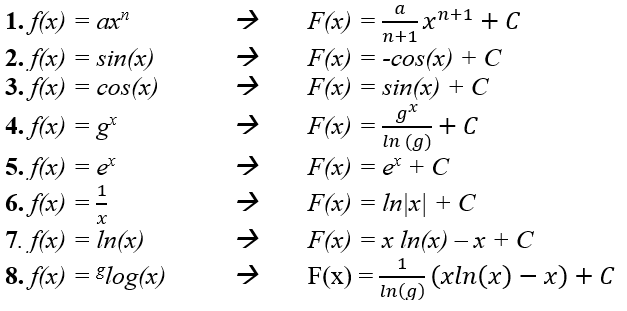
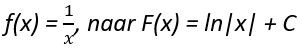 krijg je absolute waardestrepen. Dit houdt in dat de waarde niet negatief kan worden. In veel vakken, zoals
krijg je absolute waardestrepen. Dit houdt in dat de waarde niet negatief kan worden. In veel vakken, zoals