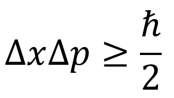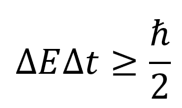De onzekerheidsrelatie van Heisenberg

Je hebt vast wel eens gehoord dat je in de kwantummechanica niet tegelijkertijd de plaats en de snelheid van een deeltje kan weten. Dit komt door de onzekerheidsrelatie. Maar hoe werkt deze relatie precies? En geldt deze alleen voor plaats en snelheid of zijn er andere combinaties mogelijk? In dit artikel lees je alles over de onzekerheidsrelatie van Heisenberg.

Video

Wil je uitleg op video zien over de onzekerheidsrelatie van Heisenberg? Kijk dan onderstaande video van natuurkundedocent Meneer Wietsma.

 

Wat is de onzekerheidsrelatie van Heisenberg?

In 1927 publiceerde Werner Heisenberg een artikel met daarin zijn bekende onzekerheidsrelatie en formuleerde deze als volgt:

De onzekerheidsrelatie houdt in dat je de positie van een deeltje x en de impuls ervan p niet tegelijkertijd kan meten met oneindige precisie. Het product van de onzekerheid op beide grootheden is altijd gelijk aan of groter dan ℏ/2. Met andere woorden: zodra je de positie van een deeltje nauwkeurig weet, heb je geen idee meer waar het deeltje heen gaat. Andersom werkt het ook: als je nauwkeurig weet waar een deeltje heen gaat, dan kun je dus onmogelijk weten waar het deeltje is. Natuurlijk kwam deze relatie niet uit het niets vallen. Hij heeft veel te maken met de golf-deeltje-dualiteit die we in de kwantummechanica kennen, waardoor deeltjes zich voor kunnen doen als golven.

Voorbeeld

Laten we naar een voorbeeld kijken om te zien hoe de onzekerheidsrelatie uit de golf-deeltjedualiteit voortkomt. Als je een grote steen in een sloot gooit, dan komen er golven die zich rondom uitbreiden van de plek waar de steen het water raakte. Omdat sommige delen van de golf zich iets sneller voortplanten dan anderen, zul je zien dat bepaalde delen van de golf zich al verder hebben voortgeplant dan andere delen. De golf spreidt dus uit doordat deze niet een exacte snelheid heeft, maar een bereik van snelheden. Hoe groter we de golf maken, hoe groter het verschil in snelheden zal zijn. Na een paar seconden kun je al zien dat de golf niet meer zo groot en dun is, maar juist erg klein en uitgespreid. In het begin kunnen we heel nauwkeurig de plek van de golf bepalen, maar de snelheid ervan niet, wat resulteert in het uitspreiden van de golf. Het omgekeerde is ook mogelijk: stel we willen graag de snelheid van de golf bepalen. Dat is zeker mogelijk als we ervoor kunnen zorgen dat golf zijn vorm behoudt. We doen dit door de golf te beschrijven als een sinusgolf, die zijn vorm behoudt terwijl de golf zich met een vaste snelheid voortplant. Nu weten we dus nauwkeurig de snelheid van de golf, maar zijn we de informatie over zijn positie kwijt, omdat een sinusgolf meerdere pieken heeft.

Dit voorbeeld is heel vergelijkbaar met wat we vinden in de kwantummechanica, waar we deeltjes beschrijven met zogeheten golffuncties. Deze golffuncties gedragen zich vergelijkbaar met de watergolven uit het voorbeeld. We kunnen dus onmogelijk zowel de positie als de snelheid van een deeltje nauwkeurig weten.

Onzekerheidsrelatie tussen energie en tijd

Naast een onzekerheidsrelatie voor positie en impuls, kunnen we er nog veel meer maken. Echter zijn deze vaak niet belangrijk in de experimenten die we doen, of hebben ze erg weinig betekenis. Een onzekerheidsrelatie die wel erg belangrijk is, is die tussen energie en tijd:

Deze zegt ons dat een deeltje tijdelijk meer energie kan hebben dan hij eigenlijk heeft. Hoe meer energie het deeltje leent, hoe korter dit mogelijk is. De gevolgen van deze relatie tussen energie en tijd zijn groot, het vormt namelijk de basis voor het quantum-tunneleffect. Het verklaart waarom een deeltje toch over een barrière heen kan komen waar het eigenlijk niet genoeg energie voor heeft. Het deeltje leent simpelweg wat energie om erover te komen! Het legt ook meteen uit waarom de kans erg klein is als de barrière erg hoog is. Het deeltje moet dan namelijk veel energie lenen, wat het maar heel kort kan hebben en daardoor dus weinig tijd heeft om over de barrière heen te komen, waardoor het niet altijd lukt.