Het quantum-tunneleffect: wat is dat?

Het quantum-tunneleffect, misschien heb je er wel eens iets over gehoord. Maar wat is het precies? En hoe komt het voort uit de gekke wereld van de kwantummechanica? In dit artikel leer je meer over het quantum-tunneleffect.

Video

Wil je een uitlegvideo zien over het quantum-tunneleffect? Kijk dan onderstaande video van natuurkundedocent meneer Wietsma.

Kwantummechanica

Laten we beginnen met een voorbeeld. Neem een bal die van een berg afrolt en het dal bereikt, waarna het weer tegen een nieuwe berg omhoog rolt. Als de bal niet snel genoeg rolt, dan zal deze nooit de andere kant van de berg bereiken omdat de bal er simpelweg niet overheen kan rollen. Als de bal geen wrijving ondervindt, zal de bal eeuwig heen en weer blijven rollen in het dal tussen de twee bergen. Dit is weergegeven in het plaatje hieronder. Om het iets abstracter te maken kunnen we de bal vervangen door een willekeurig deeltje en de berg waar de bal tegenop rolt wordt een barrière waar het deeltje normaal gesproken niet overheen kan komen omdat het deeltje niet genoeg energie heeft. We spreken nu van een deeltje dat zich in een put bevindt, waar het normaal gesproken niet uit kan komen.

In de kwantummechanica werkt het allemaal een beetje anders. Hier hebben we namelijk de dualiteit tussen een golf en een deeltje. Met andere woorden: een deeltje kan ook gezien worden als een golf en vice versa. Een deeltje kan dus worden beschreven met een golffunctie. Deze golffunctie bepaalt hoe waarschijnlijk het is dat een deeltje zich op een bepaalde plek kan bevinden. Als we teruggaan naar het deeltje in de put, dan kunnen we hiervoor een golffunctie opschrijven. Deze golffunctie is weergegeven in het plaatje hieronder. Zodra de golffunctie een muur bereikt, waar het deeltje niet genoeg energie heeft om overheen te komen, dan zou de golffunctie normaal direct naar 0 gaan. Het deeltje kan zich nooit in de muur of daarbuiten bevinden, omdat het niet genoeg energie heeft. Wiskundig gezien is dit echter niet mogelijk door de schrödingervergelijking. De golffunctie kan niet abrupt naar 0 gaan; het moet vloeiend gebeuren. Er is dus nog steeds een kans dat het deeltje zich in de muur bevindt. De golffunctie neemt vloeiend af in de barrière, als de barrière niet hoog en breed genoeg is, zal de golffunctie dus nog niet helemaal 0 zijn wanneer deze het einde van de muur bereikt. Dit betekent dus dat er een kans is dat het deeltje zich aan de andere kant van de muur kan bevinden, ook al is dit normaal gesproken niet mogelijk. Het verschijnsel dat het deeltje zich door de barrière beweegt terwijl dit niet mogelijk zou zijn noemen we het quantum-tunneleffect.

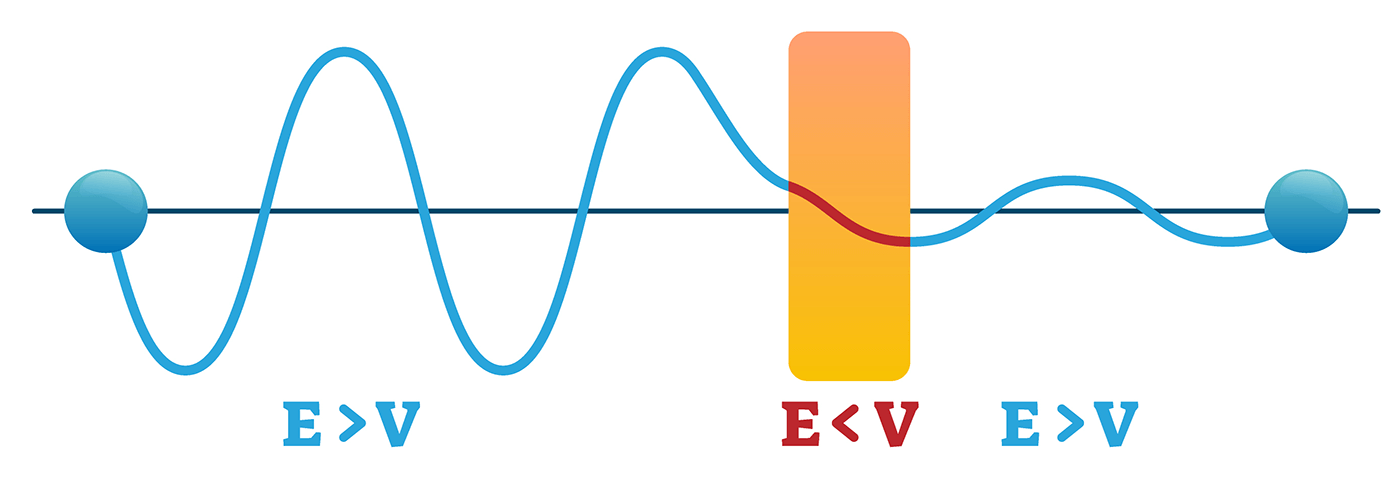
Quantum-tunneleffect in de praktijk

Omdat de snelheid waarmee de golffunctie in de barrière afneemt sterk samenhangt met de hoogte van de barrière hangt de kans om het deeltje aan de andere kant ervan te vinden sterk af van de hoogte, maar ook de breedte van de barrière. Hoe hoger en breder de barrière, hoe kleiner de kans dat het deeltje erdoorheen kan tunnelen. Hoewel het tunnelen een puur theoretisch en wiskundig verschijnsel is, is het daadwerkelijk waargenomen in experimenten. Het tunneleffect kan namelijk zeer goed verklaren hoe een vervallende atoomkern een alfadeeltje kan uitzenden, omdat dit klassiek gezien niet mogelijk is. Ook heeft het tunneleffect ons zogeheten scanning tunneling microscopen gebracht, waarmee we zeer nauwkeurig de kleinste structuren kunnen bestuderen.