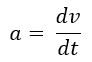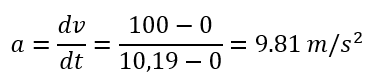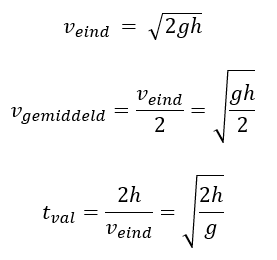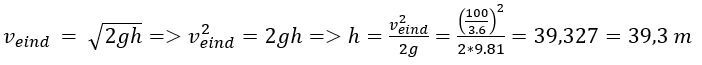Snelheid: alles wat je moet weten
Snelheid kom je overal tegen: op de fiets naar school, op de snelweg en bij een vliegtuig dat boven je langs vliegt. In dit artikel leggen we je alles uit over snelheid: van de basis tot snelheid omrekenen en de vrije val.

Wat is snelheid?

Snelheid is verandering van plaats per tijdseenheid. Het gaat hierbij over twee begrippen: plaats en snelheid. Beide hebben een grootte en een richting, het zijn dus vectorgrootheden. Je berekent de snelheid door de afgelegde afstand te delen door de benodigde tijd.
Dit is de formule van snelheid:
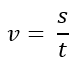
Hierin is:
- v de snelheid in meters per seconde (m/s)
- s de afstand in meter
- t de tijd in seconden
Voorbeeld:
Peter rijdt over de A10 en komt langs een hectometerpaal. Hij is benieuwd hoe snel hij rijdt, dus hij telt hoeveel seconden hij erover doet om langs de 10 volgende hectometerpaaltjes te rijden. Een hectometerpaal staat om de 100 meter. Hij telt precies 30 seconden.
De berekening ziet er dan als volgt uit:
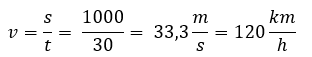
Als je jezelf afvraagt hoe je precies van 33,3 meter per seconde naar 120 kilometer per uur gaat: daar komen we zo op.
Afstand
Er is een belangrijk verschil tussen afgelegde afstand en verplaatsing. Wie van punt A naar punt B gaat en vervolgens terug naar punt A, heeft afstand gemaakt. Je bent weer terug op het punt waar je bent begonnen, waardoor je verplaatsing dus 0 is. Die verplaatsing noemen we Δs. Door onderscheid te maken tussen afgelegde afstand en verplaatsing kan er geen verwarring ontstaan over wat je precies berekent.
Hoe kan ik de snelheid en afstand aflezen uit een diagram?

Aan de hand van een diagram kun je snel informatie aflezen over tijd, snelheid en afstand. Hieronder leggen we twee veelgebruikte diagrammen uit.
Snelheid-tijdsdiagram (v,t)
In een v,t-diagram staat de tijd (t) op de horizontale as en de snelheid (v) op de verticale as. De helling van het v,t-diagram is de versnelling (a). Bij een horizontale lijn is er sprake van een constante snelheid. Bij een stijgende lijn is a > 0 en is er sprake van een versnelling. Bij een dalende lijn is a < 0 en is er sprake van een vertraging.
Voorbeeld
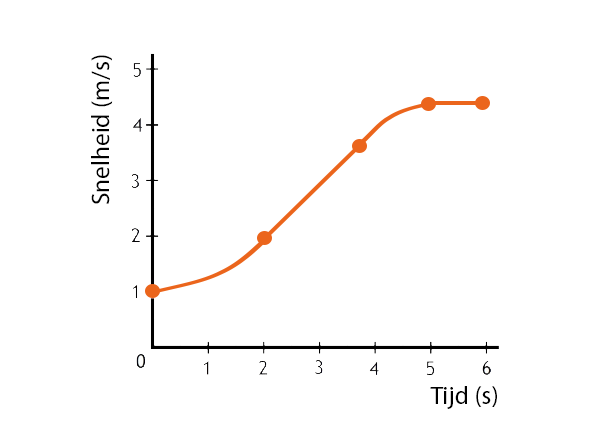
In dit v,t-diagram is te zien dat er eerst een versnelling is. Daarna gaat de lijn omhoog, maar hij blijft even steil. Er is dus sprake van een constante snelheid. Daarna gaat de lijn steeds minder steil en is er sprake van een vertraging. Aan het einde is er weer een constante snelheid, want de lijn is horizontaal.
Hoe gebruik ik de oppervlaktemethode bij een v,t-diagram?
De afgelegde afstand tussen twee tijden is te berekenen met de oppervlaktemethode. Hiervoor gebruik je de oppervlakte onder de grafiek in het v,t-diagram. Bij een constante snelheid is dit een driehoek en kun je 0,5 x hoogte x basis gebruiken. Als de grafiek een kromme lijn is, schat je de oppervlakte door zo nauwkeurig mogelijk hokjes te tellen.
Afstand-tijdsdiagram (s,t)
In een s,t-diagram staat de tijd (t) op de horizontale as en de afstand (s) op de verticale as. De helling van de grafiek vertelt je de snelheid. Een horizontale lijn betekent dat de afstand (s) niet verandert en de snelheid 0 is. Een rechte lijn met gelijke helling geeft een constante snelheid, een kromme lijn betekent dat de snelheid verandert. Hoe steiler de lijn, hoe groter de snelheid.
Voorbeeld
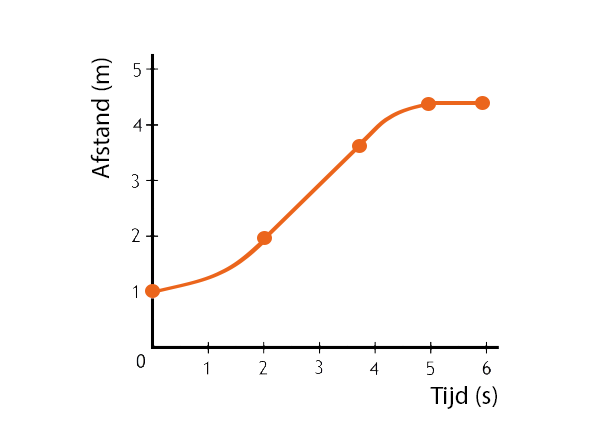
Dit s,t-diagram heeft dezelfde opbouw als het v,t-diagram. Eerst is er een versnelling, daarna is er een constante snelheid. Vervolgens wordt de lijn minder steil, de snelheid vermindert. Daarna is er een horizontale lijn, de afstand verandert niet en de snelheid is dus 0. Het voorwerp staat stil.
Hoe gebruik ik de raaklijnmethode?
Je kunt een raaklijn gebruiken om in een v,t-diagram de versnelling te bepalen en in een s,t-diagram de snelheid. Kies een tijdstip t, teken daar een raaklijn tegenaan en bereken het hellingsgetal (Δv / Δt) of (Δs / Δt).
Hoe reken je snelheid om?

In het dagelijks leven wordt snelheid vaak uitgedrukt in m/s of km/h. Omrekenen doe je heel makkelijk met één factor: 3,6.
- m/s naar km/h = × 3,6
- km/h naar m/s = / 3,6
Die 3,6 is eigenlijk heel logisch. In één uur zitten namelijk 60 minuten van 60 seconden. Oftewel, er zitten 60 · 60 = 3600 seconden in één uur. Let op: bij het omrekenen van m/s naar km/h of andersom gebruik je geen 3600, maar 3,6. De reden hiervoor is dat er 1000 meter in één kilometer zitten. Hierdoor moet je 3600 delen door 1000, waarna de factor uitkomt op 3,6.
Voorbeelden:
- Een racepaard behaalt op de renbaan een snelheid van 24 m/s. Bereken de snelheid van het paard in km/h.
Berekening: 24 · 3,6 = 86,4 km/h. - Een auto rijdt op de snelweg en gaat 80 km/h. Bereken hoeveel meter per seconde de auto aflegt bij deze snelheid.
Berekening: 80 / 3,6 = 22,2 m/s.
Wat zijn bekende soorten snelheden?

Niet alle snelheden spelen zich af op het niveau van auto's en racepaarden. Sommige zijn zó groot dat je het eigenlijk niet kunt beseffen. Hieronder hebben we drie bekende soorten snelheden voor je op een rijtje gezet.
Niets is sneller dan de snelheid van het licht. In vacuüm beweegt licht met c = 299.792.458 m/s, oftewel 300.000 kilometer per seconde.
Zoals je ziet wordt de snelheid van het licht aangegeven met een c in plaats van met een v. Dit is het geval bij natuurkundige formules zoals de massa-energierelatie van Albert Einstein: E = mc2. De lichtsnelheid is dan ook erg belangrijk in de relativiteitstheorie. Wanneer een object dichtbij de lichtsnelheid komt, kan hij voor een waarnemer vervormen.
De snelheid van het geluid is minder hoog dan de snelheid van het licht: geluid verplaatst zich in de lucht bij kamertemperatuur namelijk met 343 m/s. Dat merk je bij onweer: het licht van de bliksem is direct zichtbaar, maar de donder hoor je later. Tel je vier seconden tussen flits en knal, dan is de bliksem 343 · 4 = 1.372 meter bij je vandaan.
Alles wat sneller gaat dan geluid heeft een supersonische snelheid. Denk aan een straaljager die de geluidsbarrière doorbreekt omdat hij sneller dan 343 m/s gaat. Zo ontstaat er een schokgolf en een harde knal.
Wat is versnelling?

In de mechanica is versnelling de verandering van de snelheid van een object per tijdseenheid. Versnelling wordt vaak gezien als iets dat een voorwerp sneller laat bewegen. Echter, het gaat om een verandering van snelheid, wat dus ook een vertraging kan zijn. In dat geval spreek je van een negatieve versnelling. Deze veranderingen in tijd kunnen worden aangeduid met de volgende formule:
Hierbij is:
- a de versnelling in m/s2.
- dv de verandering in snelheid
- dt de verandering in tijd
Voorbeeld:
Joe Biden gooit een knikker van The Empire State Building af. Hij wil namelijk weten met welke versnelling de knikker naar beneden valt en of deze overeenkomt met de valversnelling op aarde: g = 9,81 m/s2. De knikker komt met een snelheid van 100 m/s op de grond neer en deed hier exact 10,19 seconden over.
Je kunt de versnelling dan als volgt berekenen:
Dit komt overeen met de valversnelling op aarde.
Video
Wil je meer weten over versnelling? Check dan zeker deze uitlegvideo:
Wat is een vrije val?

Je spreekt van een vrije val in een siutatie waarin alleen de zwaartekracht werkt. Zonder luchtweerstand, motor of menselijke krachten die tegenwerken dus. In dat scenario is de versnelling constant en gelijk aan de zwaartekracht.
In de echte wereld is er vrijwel altijd luchtweerstand. Als dit niet het geval zou zijn, zou iemand die uit het vliegtuig springt zich in een vrije val bevinden.
Een vrije val kan ook worden gecreëerd om een gevoel van gewichtloosheid te laten ervaren. Denk hierbij aan een training voor astronauten. Hiervoor wordt een vliegtuig in een paraboolbaan gebracht, waardoor deze in vrije val belandt.
Hoe bereken je de snelheid van een vrije val?

Om de snelheid te berekenen van een vrije val zonder weerstand, worden de volgende parameters gebruikt:
- g: zwaartekrachtsversnelling
- h: hoogte van de sprong in meters
- v: snelheid
- m: massa van het lichaam
- potentiële energie: mgh
- kinetische energie: mv2/2
Wanneer er geen luchtweerstand is, zijn deze laatstgenoemde twee energievormen gelijk aan elkaar. Dit komt door de wet van behoud van energie. Hiermee kunnen de snelheid bij het neerkomen veind, de gemiddelde snelheid vgemiddelde en de valduur tval worden berekend:
Voorbeeld:
Je gaat met je vader skydiven. Hij vindt het erg spannend en wil niet neerstorten wanneer zijn parachute niet opengaat. Om dit op te lossen maak je een vangnet, die hem met een snelheid van 100 km/h nog opvangt. Wat is de maximale hoogte waarop jouw vader nog uit het vliegtuig kan springen, maar wel tegengehouden wordt door het net?
De berekening ziet er als volgt uit:
Veelgestelde vragen
De snelheid (v) bereken je door de afgelegde afstand (s) te delen door tijd (t): v = s / t.
Hiervoor gebruik je de factor 3,6. Van m/s naar km/h vermenigvuldig je met 3,6 en van km/h naar m/s deel je door 3,6.
Snelheid zegt hoe hard je gaat, versnelling zegt hoe snel die snelheid verandert. De snelheid hoeft niet per se sneller te gaan. Er kan ook sprake zijn van een negatieve versnelling, oftewel een vertraging.
In vacuüm is de lichtsnelheid c = 299.792.458 m/s, vaak benoemd als 300.000 kilometer per seconde.
Geluid in de lucht bij kamertemperatuur verplaatst zich met 343 m/s. Als iets sneller dan het geluid gaat, spreken we van een supersonische snelheid.
Er is sprake van een vrije val wanneer alleen de zwaartekracht werkt en er geen andere tegenwerkende krachten werken, zoals luchtweerstand.