Alles over de normaalkracht
De normaalkracht is een veelvoorkomende kracht. Je moet hem altijd tekenen wanneer je een diagram maakt met alle krachten die op een voorwerp worden uitgeoefend. In dit artikel lees je alles wat je over de normaalkracht moet weten.

Video
Wil je liever uitleg op video? Check dan onderstaande video over de normaalkracht.
Wat is de normaalkracht?
Wanneer je op de vloer staat, dan duw je met jouw gewicht op de vloer. Toch zak je (meestal) niet door de vloer. Dit komt doordat de vloer terug duwt. De kracht waarmee de vloer terug duwt noemen we de normaalkracht. De normaalkracht staat altijd loodrecht op de oppervlakte waar je op staat, zelfs als je op een helling staat. Hier komt ook de naam normaalkracht vandaan: normaal is namelijk een ander woord voor loodrecht.
Er moet contact zijn om een normaalkracht te creëren. Het aangrijpingspunt van de normaalkracht is daarom ook het punt waar een voorwerp contact heeft met het oppervlakte waarop het ligt.
Rekenen en tekenen met de normaalkracht

Nu we weten wat de normaalkracht is en dat hij altijd loodrecht op het raakvlak werkt, kunnen we er daadwerkelijk mee gaan rekenen.
Voorbeeld 1
Een blok met een gewicht van 10 kg ligt stil op de vloer. Teken de krachten die erop uitgeoefend worden en bereken de grootte ervan.
De krachten die op het blok werken zijn de zwaartekracht en de normaalkracht, die ervoor zorgt dat het blokje niet door de vloer heen zakt. Wanneer je ze tekent, ziet het er als volgt uit:
Figuur 1: Krachten op een blok dat stil op een horizontale vloer ligt.
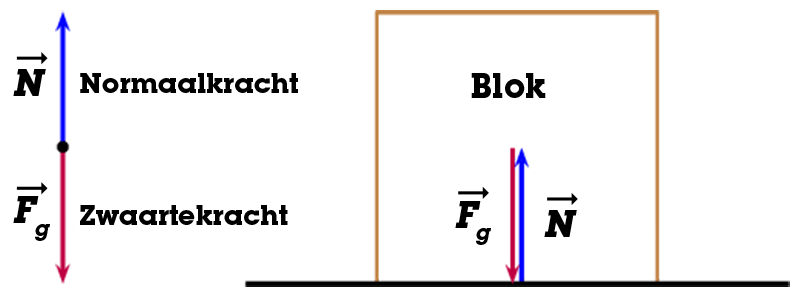
De zwaartekracht is getekend vanaf het middelpunt van het blok. Dit is namelijk het zwaartepunt en dat is het aangrijpingspunt van de zwaartekracht. De grootte van de zwaartekracht is gelijk aan de massa keer de valversnelling, dus Fg = m · g = 10 kg · 9,8 m/s2 = 98 N. Dan voor de normaalkracht: deze is getekend vanaf het punt waar het blok de vloer raakt en de grootte is exact even groot als de zwaartekracht, anders zou het blok door de grond zakken. De richting van de normaalkracht is tegengesteld aan de zwaartekracht. Als je nu de normaalkracht en de zwaartekracht bij elkaar optelt kom je uit op 0, wat klopt want het blok ligt stil.
Voorbeeld 2
Een blok ligt op een helling, zie de figuur hieronder. De helling maakt een hoek θ met de vloer. Teken de krachten die op het blok uitgeoefend worden en bereken de grootte ervan. Voor de massa van het blok neem je een waarde aan van m.
Figuur 2: Krachten die werken op een blok dat stil ligt op een helling
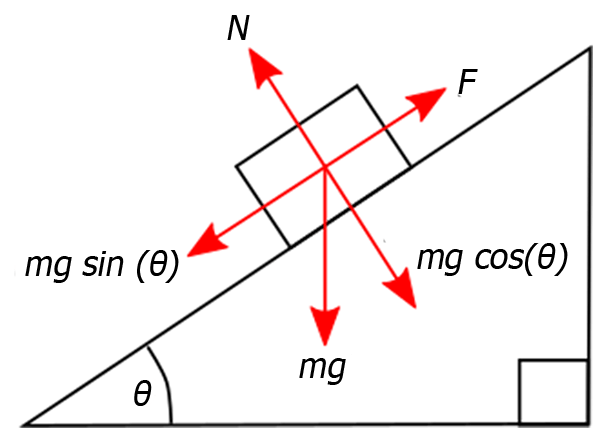
De kracht die altijd wordt uitgeoefend op het blok is de zwaartekracht, die altijd loodrecht naar beneden wijst. Daarnaast weten we dat er een normaalkracht loodrecht vanaf de helling wijst, zie de figuur. Om beter inzicht te krijgen in de situatie ontbinden we de zwaartekracht in componenten. één component staat loodrecht op de helling, m · g · cos(θ), terwijl de andere parallel aan de helling staat, m · g · sin(θ). We kunnen nu aflezen dat de normaalkracht even groot moet zijn als de loodrechte component van de zwaartekracht en in tegengestelde richting wijst. De parallelle component zou er in dit geval voor zorgen dat het blok van de helling naar beneden glijdt. Gelukkig hebben we nog een wrijvingskracht aangeduid met F in de figuur. Deze wrijvingskracht wijst tegengesteld aan de parallelle component van de zwaartekracht met dezelfde grootte en zorgt er dus voor dat het blokje blijft liggen waar het ligt.









