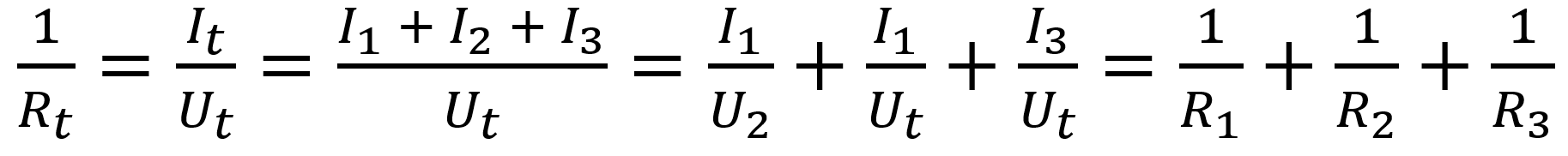Alles over serie- en parallelschakelingen

Als je wel eens met elektrische schakelingen hebt gewerkt, dan ben je vast de termen serie- en parallelschakeling tegengekomen. In dit artikel lees je alles wat je moet weten over de verschillen tussen deze twee en hoe je ermee rekent.

Serieschakelingen

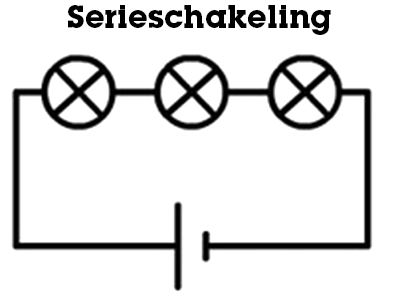
Als verschillende elektrische componenten in serie zijn geschakeld, dan wil dit zeggen dat de componenten achter elkaar aan zijn geschakeld. Zie het als een lange kralenketting, waarin de draad van de ketting in dit geval de stroomdraad voorstelt en de kralen de elektrische componenten. Een voorbeeld van een serieschakeling zijn de lampjes in een kerstboom. Het grootste probleem met een serieschakeling is dat als er één component stuk gaat, de stroomkring verbroken is en daardoor alle andere componenten ook niet meer werken. Hieronder zie je een tekening van een serieschakeling.

Figuur 1: Een simpele serieschakeling van lampjes en een spanningsbron

Componenten die in serie zijn geschakeld, kun je ook vervangen door één component. De regels hiervoor zijn als volgt:

• De stroomsterkte door elk van de componenten is hetzelfde. Als we de lampjes hierboven zouden nummeren van links naar rechts krijgen we: I_t = I₁ = I₂ = I₃ waarin I_t de stroom is die wordt geleverd door de spanningsbron.
• De spanning op de verschillende componenten tellen bij elkaar op: U_t = U₁ + U₂ + U₃. Oftewel: de som van de spanning van de componenten kan nooit meer zijn dan de spanning die wordt geleverd door de bron. Als je meerdere batterijen in serie schakelt, dan kun je dus een grote spanning opwekken doordat de spanning van componenten in serie bij elkaar optelt.
• De weerstand van de verschillende componenten tel je bij elkaar op: R_t = R₁ + R₂ + R₃. Je kunt dit ook afleiden uit de formule voor de weerstand R = U / I en het feit dat de spanning U bij elkaar optelt, terwijl de stroomsterkte I gelijk blijft.

Rekenen met serieschakelingen

Neem bovenstaand schakelschema. De spanningsbron levert 12 V en 5 A. De weerstand van het eerste lampje is 1 Ω en op het tweede lampje staat een spanning van 3 V. Bereken de weerstand van het tweede lampje en de weerstand van en de spanning op het derde lampje.

Met de formule voor de weerstand R = U ּ· I kunnen we alles oplossen in dit schakelschema. We weten dat de spanning van de individuele componenten bij elkaar opgeteld niet meer kan zijn dan de spanning geleverd door de spanningsbron en de stroomsterkte door alle componenten gelijk is aan 5 A.

Voor het eerste lampje hebben we R₁ = U₁ / I, waarmee we kunnen berekenen: U₁ = I · R₁ = 5A · 1 Ω.

Voor R₂ kunnen we invullen R₂ = (U₂ / I) = (3 V / 5 A) = 0,6 Ω.

Nu weten we dus U_t = U₁ + U₂ + U₃ → U₂ + U₃ = U_t - U₁ = 12 V - 5 V = 7 V.

Omdat U₂ = 3 V weten we dus dat U₃ = 4 V.

Nu hebben we dus alles om R₃ te berekenen: R₃ = (U₃ / I) = (4 V / 5 A) = 0,8 Ω.

Parallelschakelingen

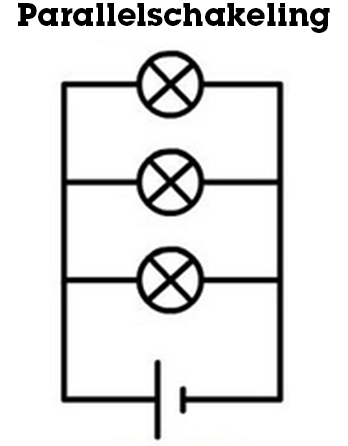
In een parallelschakeling zijn componenten naast elkaar geschakeld. Je kunt dit zien als een grote straat met kleine zijstraten; de zijstraten zijn dan de componenten en komen aan het einde weer uit op een andere grote straat. Hieronder zie je een schakelschema van 3 lampjes en een spanningsbron die parallel zijn geschakeld.

Figuur 2: Een parallelschakeling met lampjes en een spanningsbron

Het voordeel van een parallelschakeling ten opzichte van een serieschakeling is het feit dat wanneer 1 component stuk gaat, de andere componenten nog wel een gesloten stroomkring vormen en dus blijven werken. De rekenregels voor parallelschakelingen zijn:

• De stroomsterkte door de verschillende componenten tel je bij elkaar op: I_t = I₁ + I₂ + I₃. Zie het als auto’s die afslaan van een straat: er kunnen nooit meer auto’s uit een straat komen dan er ingaan.
• De spanning over de verschillende componenten is altijd gelijk: U_t = U₁ = U₂ = U₃.
• De weerstand van de componenten is dan als volgt:

Rekenen met parallelschakelingen

Neem bovenstaand schakelschema van de parallelschakeling. De spanningsbron levert 12 V en de weerstand van het onderste lampje is 20 Ω. De stroomsterkte door het tweede lampje is 2 A en de weerstand van het derde lampje is 15 Ω. Bereken de stroomsterkte die de spanningsbron levert.

In deze vraag gebruiken we het feit dat in een parallelschakeling, de stroomsterkte door de verschillende componenten bij elkaar optelt en de spanning over alle componenten hetzelfde is.

Voor het eerste lampje kunnen we de stroomsterkte uitrekenen: I₁ = U / R₁ = 12 V / 20 Ω = 0,6 A.

Dit is het eerste stukje van de totale stroomsterkte.

Voor het tweede lampje is de stroomsterkte gegeven: 2 A. We kunnen nog de weerstand uitrekenen, maar dat wordt in dit geval niet gevraagd, dus slaan we dit over.

Van het derde lampje is de weerstand gegeven, dus we kunnen de stroomsterkte door dit lampje uitrekenen op dezelfde manier als voor het eerste lampje: I₃ = U / R₃ = 12 / 15 Ω = 0,8 A.

Nu we de stroomsterkte door alle componenten hebben, kunnen we de totale stroomsterkte uitrekenen.

Dit is dan ook meteen de stroomsterkte die de bron moet leveren: I_t = I₁ + I₂ + I₃ = 0,6 A + 2 A + 0,8 A = 3,4 A.

De stroomsterkte die de bron levert is dus 3,4 A.